题目内容
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:从原点O到(2,-1)的“出租车距离”为3,最短路线有3条;
从原点O到(2,2)的“出租车距离”为4,最短路线有6条.
(1)①从原点O到(6,1)的“出租车距离”为______.最短路线有______条;
②与原点O的“出租车距离”等于30的路口共有______个.
(2)①解释应用:从原点O到坐标(n,2)(n为大于2的整数)的路口A,有多少条最短路线?(请给出适当的说理或过程)
②解决问题:
从坐标为(1,-2)的路口到坐标为(3,36)的路口,最短路线有______条.

【答案】分析:(1)①根据题目信息,“出租车距离”等于点的横坐标与纵坐标绝对值的和,进行计算即可求解;
②平面被坐标系分4个区域,在每一个区域内与原点0的“出租车距离”等于30的街区(m,n)满足 m,n都是正整数,|m|+|n|=30,对于m的任意取值,n都有唯一的正整数和它对应,所以m可取30个值,n有30个值和它对应,然后即可求解;
(2)①出租车从原点O到坐标(n,2)(n为大于2的整数)的街区,需走(n+2)路程,不论横坐标与纵坐标,没确定一个单位的走法,则还剩下(n+2-1)种走法,依此类推,进行计算即可;
②把原点坐标平移到(1,-2),则点(3,36)的坐标变为(2,38),然后根据①中的结论进行计算即可.
解答:解:(1)①6+1=7,7;
②与原点0的“出租车距离”等于30的街区(m,n)满足m,n都是正整数,|m|+|n|=30,
由对称性,考虑m>0,n>,
m依次取1,2,…30,对应的n为29,28,…,0,共30个,
∴与原点0的“出租车距离”等于30的街区共30×4=120个;
(2)①从原点O到坐标(n,2)的“出租车距离”为n+2,
则最短路线的条数是(n+2-1)+(n+2-2)+(n+2-3)+…+1,
=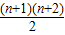 ;
;
②把原点坐标平移到(1,-2),则点(3,36)的坐标变为(2,38),
∴“出租车距离”为2+38=40,
∴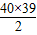 =780.
=780.
故答案为:(1)①7,7;②120;(2)①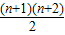 ;②780.
;②780.
点评:本题考查理解题意能力以及看图能力,关键是明白怎样是“出租车距离”和路线的走法.
②平面被坐标系分4个区域,在每一个区域内与原点0的“出租车距离”等于30的街区(m,n)满足 m,n都是正整数,|m|+|n|=30,对于m的任意取值,n都有唯一的正整数和它对应,所以m可取30个值,n有30个值和它对应,然后即可求解;
(2)①出租车从原点O到坐标(n,2)(n为大于2的整数)的街区,需走(n+2)路程,不论横坐标与纵坐标,没确定一个单位的走法,则还剩下(n+2-1)种走法,依此类推,进行计算即可;
②把原点坐标平移到(1,-2),则点(3,36)的坐标变为(2,38),然后根据①中的结论进行计算即可.
解答:解:(1)①6+1=7,7;
②与原点0的“出租车距离”等于30的街区(m,n)满足m,n都是正整数,|m|+|n|=30,
由对称性,考虑m>0,n>,
m依次取1,2,…30,对应的n为29,28,…,0,共30个,
∴与原点0的“出租车距离”等于30的街区共30×4=120个;
(2)①从原点O到坐标(n,2)的“出租车距离”为n+2,
则最短路线的条数是(n+2-1)+(n+2-2)+(n+2-3)+…+1,
=
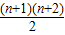 ;
;②把原点坐标平移到(1,-2),则点(3,36)的坐标变为(2,38),
∴“出租车距离”为2+38=40,
∴
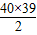 =780.
=780.故答案为:(1)①7,7;②120;(2)①
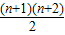 ;②780.
;②780.点评:本题考查理解题意能力以及看图能力,关键是明白怎样是“出租车距离”和路线的走法.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.