题目内容
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,A(1,0)、C(0,7).
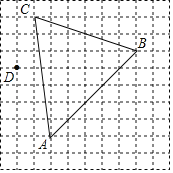
(1)在方格纸中画出平面直角坐标系,写出B点的坐标:B ;
(2)直接写出△ABC的形状: ,直接写出△ABC的面积 ;
(3)若D(﹣1,4),连接BD交AC于E,则![]() = .
= .
【答案】(1)如图,见解析;(6,5);(2)等腰三角形;20;(3)![]() .
.
【解析】
(1)利用A点和C点坐标画出x轴与y轴,然后写出B点坐标;
(2)根据勾股定理得到AC=![]() =5
=5![]() ,AB=
,AB=![]() =5
=5![]() ,求得△ABC是等腰三角形,根据三角形的面积=长方形的面积-3个三角形的面积即可得到结论;
,求得△ABC是等腰三角形,根据三角形的面积=长方形的面积-3个三角形的面积即可得到结论;
(3)设BD与y轴交于H,过B作BF⊥y轴于F,连接CD,根据勾股定理的逆定理得到∠DCB=90°,根据相似三角形的判定与性质即可得到结论.
(1)如图,建立如图所示的平面直角坐标系,
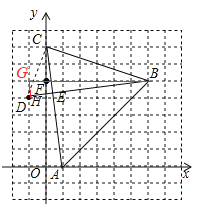
则B点的坐标为(6,5),
故答案为:(6,5);
(2)∵AC=![]() =5
=5![]() ,AB=
,AB=![]() =5
=5![]() ,
,
∴AC=AB,
∴△ABC是等腰三角形;
△ABC的面积=6×7﹣(![]() ×1×7+
×1×7+![]() ×2×6+
×2×6+![]() ×5×5)=20;
×5×5)=20;
故答案为:等腰三角形;20;
(3)设BD与y轴交于H,过B作BF⊥y轴于F,连接CD,
∵CD2=10,BC2=40,BD2=50,
∴CD2+BC2=BD2,
∴∠DCB=90°,
在△COA和△BGD中,
∴
∴△COA≌△BGD
∴∠ACO=∠DBF,∠DBF+∠BHF=90°,
∴∠ACO+∠BHF=90°
∴∠CEH=90°,
∴CE⊥BC,
在△DCE和△DBC中,
![]()
∴△DCE∽DBC
∴![]()
∴CD2=DEBD,
∴DE=![]() =
=![]() ,
,
∴BE=4![]() ,
,
∴![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目