题目内容
【题目】某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度,方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN项部M的仰角为37°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E.请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan35°≈0.75)
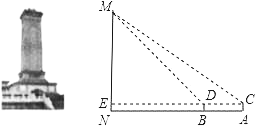
【答案】人民英雄纪念碑MN的高度约为36.5米.
【解析】
在Rt△MED中,由∠MDE=45°知ME=DE,据此设ME=DE=x,则EC=x+15,在Rt△MEC中,由ME=ECtan∠MCE知x≈0.7(x+15),解之求得x的值,根据MN=ME+EN可得答案.
由题意得四边形ABDC、ACEN是矩形,
∴EN=AC=1.5,AB=CD=15,
在Rt△MED中,∠MED=90°,∠MDE=45°,
∴ME=DE,
设ME=DE=x,则EC=x+15,
在Rt△MEC中,∠MEC=90°,∠MCE=35°,
∵ME=ECtan∠MCE,
∴x≈0.7(x+15),
解得:x≈35,
∴ME≈35,
∴MN=ME+EN≈36.5,
答:人民英雄纪念碑MN的高度约为36.5米.

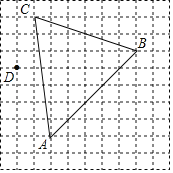
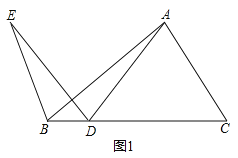
【题目】如图,在![]() 中,点D是线段
中,点D是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点D逆时针旋转90°得到线段
绕点D逆时针旋转90°得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设B,D两点间的距离为
,设B,D两点间的距离为![]() ,A,D两点间的距离为
,A,D两点间的距离为![]() ,B,E两点间的距离为
,B,E两点间的距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究
随自变量x的变化而变化的规律进行了探究
下面是小明的探究过程,请补全完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与x的几组对应值,如下表:(说明:补全表格时相关数值保留一位小数)
与x的几组对应值,如下表:(说明:补全表格时相关数值保留一位小数)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
| a | 5.66 | 4.32 | b | 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
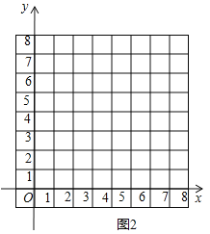
(3)结合函数图象,解决问题:
①当E在线段![]() 上时,
上时,![]() 的长度约为___________cm;
的长度约为___________cm;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度x约为___________cm.
的长度x约为___________cm.