题目内容
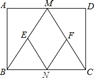
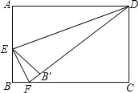
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
【答案】A
【解析】
B′的运动轨迹是以E为圆心,以AE的长为半径的圆.所以,当B′点落在DE上时,B′D取得最小值.根据勾股定理求出DE,根据折叠的性质可知B′E=BE=2,DE﹣B′E即为所求.
解:如图,B′的运动轨迹是以E为圆心,以AE的长为半径的圆.所以,当B′点落在DE上时,B′D取得最小值.

根据折叠的性质,△EBF≌△EB′F,
∴EB′⊥B′F,
∴EB′=EB,
∵E是AB边的中点,AB=4,
∴AE=EB′=2,
∵AD=6,
∴DE=![]() =2
=2![]() ,
,
∴DB′=2![]() ﹣2.
﹣2.
故选:A.

练习册系列答案
相关题目