题目内容
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).

【答案】(1)x=![]() ;(2)y=﹣
;(2)y=﹣![]() x2+
x2+![]() x;(3)证明见解析;(4)当0≤x<
x;(3)证明见解析;(4)当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.
【解析】
(1)若使PQ⊥AC,则根据路程=速度×时间表示出CP和CQ的长,再根据30度的直角三角形的性质列方程求解;
(2)首先画出符合题意的图形,再根据路程=速度×时间表示出BP,CQ的长,根据等边三角形的三线合一求得PD的长,根据30度的直角三角形的性质求得PD边上的高,再根据面积公式进行求解;
(3)根据三角形的面积公式,要证明AD平分△PQD的面积,只需证明O是PQ的中点.根据题意可以证明BP=CN,则PD=DN,再根据平行线等分线段定理即可证明;
(4)根据(1)中求得的值即可分情况进行讨论.
(1)当Q在AB上时,显然PQ不垂直于AC,
当Q在AC上时,由题意得,BP=x,CQ=2x,PC=4﹣x;
∵AB=BC=CA=4,
∴∠C=60°;
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,
∴4﹣x=2×2x,
∴x=![]() ;
;
(2)y=﹣![]() x2+
x2+![]() x,
x,
如图所示,
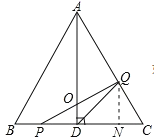
当0<x<2时,P在BD上,Q在AC上,过点Q作QN⊥BC于N;
∵∠C=60°,QC=2x,
∴QN=QC×sin60°=![]() x;
x;
∵AB=AC,AD⊥BC,
∴BD=CD=![]() BC=2,
BC=2,
∴DP=2﹣x,
∴y=![]() PDQN=
PDQN=![]() (2﹣x)
(2﹣x)![]() x=﹣
x=﹣![]() x2+
x2+![]() x;
x;
(3)当0<x<2时,
在Rt△QNC中,QC=2x,∠C=60°;
∴NC=x,
∴BP=NC,
∵BD=CD,
∴DP=DN;
∵AD⊥BC,QN⊥BC,
∴AD∥QN,
∴OP=OQ,
∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
(4)显然,不存在x的值,使得以PQ为直径的圆与AC相离,
由(1)可知,当x=![]() 时,以PQ为直径的圆与AC相切;
时,以PQ为直径的圆与AC相切;
当点Q在AB上时,
8﹣2x=![]() ,
,
解得x=![]() ,
,
故当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,
时,以PQ为直径的圆与AC相切,
当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.