Question

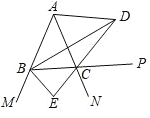
【题目】如图，∠ABC ∠ACB ，BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ，BE平分外角 ∠MBC 交 DC 的延长线于点 E ，以下结论：①∠BDE ∠BAC ；② DB⊥BE ；③∠BDC ∠ACB 90 ；④∠BAC 2∠BEC 180 .其中正确的结论有（ ）

A.1 个B.2 个C.3 个D.4 个

Answer 1

【答案】D

【解析】

根据角平分线的定义、三角形的内角和定理、三角形的外角的性质、判断即可．

① ∵BD、CD分别平分△ABC的内角∠ABC、外角∠ACP，

∴∠ACP=2∠DCP，∠ABC=2∠DBC，

又∵∠ACP=∠BAC+∠ABC，∠DCP=∠DBC+∠BDC，

∴∠BAC=2∠BDE，

∴BDE BAC

∴①正确；

②∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC，

∴∠DBE=∠DBC+∠EBC= ∠ABC+∠MBC=×180°=90°，

∴EB⊥DB，

故②正确，

③∵∠DCP=∠BDC+∠CBD，2∠DCP=∠BAC+2∠DBC，∴2(∠BDC+∠CBD)=∠BAC+2∠DBC，

∴∠BDC=∠BAC，

∵∠BAC+2∠ACB=180°，

∴∠BAC+∠ACB=90°，

∴∠BDC+∠ACB=90°，

故③正确，

④∵∠BEC=180° (∠MBC+∠NCB)

=180° (∠BAC+∠ACB+∠BAC+∠ABC)

=180° (180°+∠BAC)

∴∠BEC=90°∠BAC，

∴∠BAC+2∠BEC=180°，故④正确，

即正确的有4个，

故选D