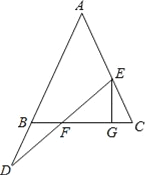
题目内容
【题目】等腰直角三角形ABC，AB=AC，∠BAC=∠BDC=90°，
（1）若∠DBA=20°，则∠ACD=______°；
（2）连接AD，则∠ADB=______°．
【答案】20； 45
【解析】
（1）利用三角形内角和定理求出∠AGB，根据对顶角相等求出∠CGD即可解决问题；
（2）由说明△CGD∽△BGA，得到
，进而得到△CGB∽△DGA，可得∠ADG=∠BCG解决问题；
解：（1）
∵∠DBA=20°，∠BAG=90°，
∴∠BGA=90°-20°=70°，
∴∠CGD=∠AGB=70°，
∵∠CDG=90°，
∴∠DCG=90°-70°=20°，
故答案为20．
（2）∵∠CGD=∠BGA，∠CDG=∠BAG=90°，
∴△CGD∽△BGA，
∴
=
，
∵∠CGB=∠DGA，
∴△CGB∽△DGA，
∴∠ADG=∠BCG，
∵AB=AC，∠BAC=90°，
∴∠ACB=45°，
∴∠ADB=∠BCG=45°，
故答案为45．
练习册系列答案
相关题目
【题目】某市在2013年义务教育质量监测过程中，为了解学生的家庭教育情况，就八年级学生平时主要和谁在一起生活进行了抽样调查．下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图．
频数分布表
代码 | 和谁一起生活 | 频数 | 频率 |
A | 父母 | 4200 | 0.7 |
B | 爷爷奶奶 | 660 | a |
C | 外公外婆 | 600 | 0.1 |
D | 其它 | b | 0.09 |
合计 | 6000 | 1 |
请根据上述信息，回答下列问题：
（1）a= ，b= ；
（2）在扇形统计图中，和外公外婆一起生活的学生所对应扇形圆心角的度数是 ；
（3）若该市八年级学生共有3万人，估计不与父母一起生活的学生有 人．
