题目内容
【题目】长方形的长为a厘米，宽为b厘米，其中a>b,如果将原长方形的长和宽各增加3厘米，得到的新长方形面积记为S1，如果将原长方形的长和宽分别减少2厘米，得到的新长方形面积记为S2．
（1）若a、b为正整数，请说明：S1与S2的差一定是5的倍数；
（2）如果S1＝2S2，求将原长方形的长和宽分别减少7厘米后得到的新长方形面积；
（3）如果用一个面积为S1的长方形和两个面积为S2的长方形恰好能没有缝隙没有重叠地拼成一个正方形，求a，b的值．
【答案】（1）见解析；（2）将原长方形的长和宽分别减少7厘米后得到的新长方形面积为50平方厘米；（3）a，b的值分别为7和4.5
【解析】
（1）分别求出S1，S2，S1﹣S2的值，从而求解；（2）由S1＝2S2，求得ab﹣7a﹣7b＝1，然后求出将原长方形的长和宽分别减少7厘米后得到的新长方形面积，最后整体代入求值即可；（3）由题意，根据拼接图形的边长之间的等量关系，列方程组求解，根据问题的实际意义作出取舍即可．
解：（1）证明：由题意得：
S1＝（a+3）（b+3）＝ab+3（a+b）+9
S2＝（a﹣2）（b﹣2）＝ab﹣2（a+b）+4
∴S1﹣S2＝ab+3（a+b）+9﹣ab+2（a+b）﹣4
＝5（a+b）+5＝5（a+b+1） ∴S1与S2的差一定是5的倍数．
（2）∵S1＝2S2，
∴ab+3a+3b+9＝2（ab﹣2a﹣2b+4）
∴ab﹣7a﹣7b-1＝0
∴ab﹣7a﹣7b＝1
∵将原长方形的长和宽分别减少7厘米后得到的新长方形面积为：
（a﹣7）（b﹣7）＝ab﹣7a﹣7b+49＝1+49＝50
∴将原长方形的长和宽分别减少7厘米后得到的新长方形面积为50平方厘米．
（3）由题意可得方程组：
①
解得
②
解得：
故该组方程组的解不符合题意
∴a，b的值分别为7和4.5
亮点激活精编提优100分大试卷系列答案【题目】已知关于x的代数式x2+bx+c，设代数式的值为y．下表中列出了当x分别取﹣1，0，1，2，3，4，5，…m，m+1…时对应的y值．
x | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | m | m+1 | |||
y | 10 | 5 | 2 | 1 | 2 | 5 | n | p | q |
（1）表中n的值为 ；
（2）当x＝ 时，y有最小值，最小值是 ；
（3）比较p与q的大小．
【题目】已知二次函数y＝ax2+bx（a≠0）中自变量x和函数值y的部分对应值如下表：
x | … | ﹣2.5 | ﹣2 | ﹣1 | 0 | 0.5 | … |
y | … | ﹣5 | 0 | 4 | 0 | ﹣5 | … |
（1）求二次函数解析式，并写出顶点坐标；
（2）在直角坐标系中画出该抛物线的图象；
（3）若该抛物线上两点A（x1，y1）、B（x2，y2）的横坐标满足x1＜x2＜﹣1，试比较y1与y2的大小，并说明理由．
【题目】为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
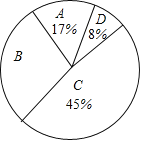
请根据所给信息，解答以下问题：
(1)表中a=___，b=___；
(2)请计算扇形统计图中B组对应扇形的圆心角的度数；
(3)已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
