题目内容
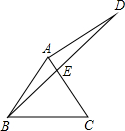
在△ABC中,BC=5,AC=12,AB=13,在AB、AC上分别取点D、E,使线段DE将△ABC分成面积相等的两部分,则这样线段的最小值是______.
∵BC2+AC2=AB2,
∴△ABC为直角三角形,
过D作DF⊥AC于F,设DF=x,则
=
,
∴AF=
x,
∵S△ADE=
x•AE=
S△ABC=15,
∴AE=
,EF=
-
x,
∴DE2=DF2+EF2=x2+(
-
x)2=
x2+
-144=(
x-
)2+12≥12,
故可得DE2最小值是12,
∴DE最小值为2
.
故答案为:2
.
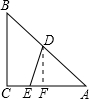
∴△ABC为直角三角形,
过D作DF⊥AC于F,设DF=x,则
| x |
| 5 |
| AF |
| 12 |
∴AF=
| 12 |
| 5 |
∵S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| 30 |
| x |
| 30 |
| x |
| 12 |
| 5 |
∴DE2=DF2+EF2=x2+(
| 30 |
| x |
| 12 |
| 5 |
| 169 |
| 25 |
| 900 |
| x2 |
| 13 |
| 5 |
| 30 |
| x |
故可得DE2最小值是12,
∴DE最小值为2
| 3 |
故答案为:2
| 3 |


练习册系列答案
相关题目