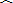题目内容
如图,△ABC中,AB=8,AC=6,BC=10,BE、CF、AG分别是中线,交于点O,则OE=______,OG=______.
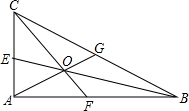

∵△ABC中,AB=8,AC=6,BC=10,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∵AG是斜边BC的中线,
∴AG=
BC=
×10=5,
∴OG=
AG=
×5=
;
∵BE是AC边的中线,
∴AE=
AC=
×6=3,
在Rt△ABE中,BE=
=
=
,
∴OE=
BE=
×
=
.
故答案为:
,
.
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∵AG是斜边BC的中线,
∴AG=
| 1 |
| 2 |
| 1 |
| 2 |
∴OG=
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
∵BE是AC边的中线,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABE中,BE=
| AB2+AE2 |
| 82+32 |
| 73 |
∴OE=
| 1 |
| 3 |
| 1 |
| 3 |
| 73 |
| ||
| 3 |
故答案为:
| ||
| 3 |
| 5 |
| 3 |

练习册系列答案
相关题目