题目内容
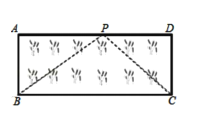
【题目】(1)如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内.
解:如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴ =AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4, =∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC= °
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
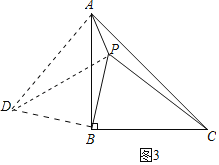
(2)如图3,在△ABC中,AB=BC,∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.
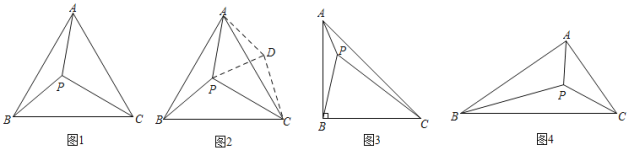
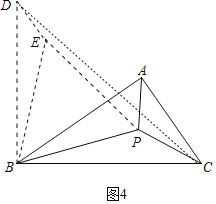
(3)拓展应用.如图4,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .
【答案】(1)PD,∠CAD,∠APB,90;(2)∠APB=135°;(3)![]() .
.
【解析】
(1)根据全等三角形的判定和性质即可解决问题;
(2)图3中,把△PBC绕B点逆时针旋转90°得到△DBA,利用勾股定理的逆定理证明∠APD=90°即可解决问题;
(3)如图4中,将△ABP绕着点B逆时针旋转60°,得到△DBE,证明△ABP≌△DBE,则∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,再证明∠DBC=90°,在Rt△BCD中,由勾股定理求出CD的长度,即为PA+PB+PC的最小值.
(1)如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴PD=AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°,
∴∠BAP=∠CAD,
∴△ABP≌△ACD(SAS)
∴BP=CD=4,∠APB=∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC=90°
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
故答案为:PD,∠CAD,∠APB,90.
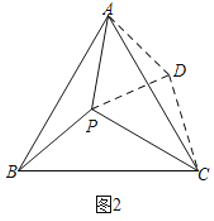
(2)解:∵∠ABC=90°,BC=AB,
∴把△PBC绕B点逆时针旋转90°得到△DBA,如图3,
∴AD=PC=3,BD=BP=2,
∵∠PBD=90°
∴DP=![]() PB=2
PB=2![]() ,∠DPB=45°,
,∠DPB=45°,
在△APD中,AD=3,PD=2![]() ,PA=1,
,PA=1,
∵12+(2![]() )2=32,
)2=32,
∴AP2+PD2=BD2,
∴△APD为直角三角形,
∴∠APD=90°,
∴∠APB=∠APD+∠DPB=90°+45°=135°.
(3)解:如图4中,将△ABP绕着点B逆时针旋转60°,得到△DBE,连接EP,CD,
∴△ABP≌△DBE
∴∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,
∴△BPE是等边三角形
∴EP=BP
∴AP+BP+PC=PC+EP+DE
∴当点D,点E,点P,点C共线时,PA+PB+PC有最小值CD
∵∠ABC=30°=∠ABP+∠PBC
∴∠DBE+∠PBC=30°
∴∠DBC=90°
∴CD=![]() ,
,
故答案为![]() .
.