题目内容
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=6,点P是斜边AB上一点(点P不与点A,B重合),过点P作PQ⊥AB于P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y.
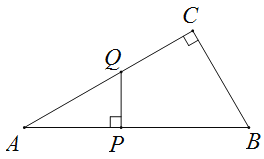
小明根据学习函数的经验,对函数y随自变量x的变换而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)通过取点、画图、测量、计算,得到了x与y的几组值,如下表:
x | …… | 0.8 | 1.0 | 1.4 | 2.0 | 3.0 | 4.0 | 4.5 | 4.8 | 5.0 | 5.5 | …… |
y | …… | 0.2 | 0.3 | 0.6 | 1.2 | 2.6 | 4.6 | 5.8 | 5.0 | m | 2.4 | …… |
经测量、计算,m的值是 (保留一位小数).
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合几何图形和函数图象直接写出,当QP=CQ时,x的值是 .
【答案】(1)4.3;(2)见解析;(3)3.0或5.2.
【解析】
(1)由表中数据变化可知,当x=AP=5.0时,点Q在BC上,如下图1,此时BP=6-5=1,由已知条件易得PQ=![]() ,再由y=S△APQ=
,再由y=S△APQ=![]() AP·PQ即可求得对应的y的值;
AP·PQ即可求得对应的y的值;
(2)根据表格中的数据描点,再用平滑的曲线将各点连接起来即可;
(3)根据题意分:①点Q在AC上;②点Q在BC上两种情况分别计算出对应的AP的值即可.
(1)∵PQ⊥AB于P,
∴∠APQ=90°,
∵∠A=30°,∠C=90°,
∴∠B=60°,
∵AB=6,AP=5.0,
∴BP=1.0
∴ PQ=![]() ,
,
∴y=S△APQ
=![]() AP·PQ
AP·PQ
=![]()
≈4.3
故答案为:4.3;

(2)根据表中数据描点,连线得到的函数图象如下图所示:

(3)∵在△ABC中,∠C=90°,∠A=30°,AB=6,
∴AC=AB·cosA=![]() ,BC=AB·sinA=
,BC=AB·sinA=![]() .
.
①如图2,当点Q在AC上时,
∵QP⊥AB,
∴∠QPA=90°,
∵∠A=30°,
∴PQ=AP·tanA=![]() ,AQ=
,AQ=![]() ,
,
又∵CQ=PQ,AC=AQ+CQ=![]() ,
,
∴![]() ,解得:
,解得:![]() ;
;

②如图3,当点Q在BC上时,
∵QP⊥AB,
∴∠QPA=90°,
∵∠B=60°,PB=AB-AP=6-x,
∴PQ=PB·tanB=![]() ,BQ=
,BQ=![]() ,
,
又∵CQ=PQ,BQ+CQ=BC=3,
∴![]() ,解得:
,解得:![]() .
.

综上所述,当QP=CQ时![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案