题目内容
【题目】如图，在平行四边形
中，
是
的中点，延长
到点
，使
，连接
，
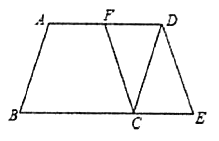
（1）求证：四边形
是平行四边形；
（2）若
，
，
，求的长.
【答案】（1）详见解析；（2）
【解析】
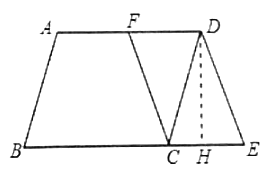
（1）由“平行四边形的对边平行且相等”的性质推知AD∥BC，且AD＝BC；然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等（DF＝CE，且DF∥CE），即四边形CEDF是平行四边形；
（2）如图，过点D作DH⊥BE于点H，构造含30度角的直角△DCH和直角△DHE．通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度．
（1）在
中，
，且
.
是
的中点，
.
又
，
，且
，
四边形
是平行四边形；
（2）如图，过点
作
于点
.
在中，
，
.
，
，
，
.
在
中，
，则
.
在
中，根据勾股定理知
.
阅读快车系列答案
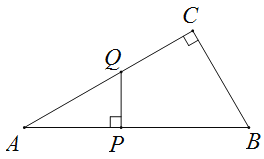
【题目】如图，△ABC中，∠ACB=90°，∠A=30°，AB=6，点P是斜边AB上一点（点P不与点A，B重合），过点P作PQ⊥AB于P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y．
小明根据学习函数的经验，对函数y随自变量x的变换而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表：
x | …… | 0.8 | 1.0 | 1.4 | 2.0 | 3.0 | 4.0 | 4.5 | 4.8 | 5.0 | 5.5 | …… |
y | …… | 0.2 | 0.3 | 0.6 | 1.2 | 2.6 | 4.6 | 5.8 | 5.0 | m | 2.4 | …… |
经测量、计算，m的值是 （保留一位小数）．
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合几何图形和函数图象直接写出，当QP=CQ时，x的值是 ．
【题目】将一些数排列成下表中的四列：
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
（1）第4行第1列的数是多少？直接写出答案；
（2）第17行的四个数之和是多少？请写出适当的过程；
（3）数100所在的行和列分别是多少？直接写出答案.
【题目】某商场春节促销活动出售
两种商品，活动方案如下两种：
方案一 |
|
| |
每件标价 | 90元 | 100元 | |
每件商品返利 | 按标价的 | 按标价的 | |
例如买一件 | |||
方案二 | 所购商品一律按标价20％的返利 | ||
（1）某单位购买
商品
件，
商品20件，选用何种方案划算？
（2）某单位购买商品件（
为正整数），购买商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少？
（3）若两种方案的实际付款一样，求的值．
