题目内容
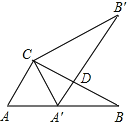
【题目】如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.![]() B.5
B.5![]() C.5D.2
C.5D.2![]()
【答案】A
【解析】
根据旋转的性质得CA=CA′=2,∠CA′B′=∠A=60°,则△CAA′为等边三角形,所以∠ACA′=60°,则可计算出∠BCA′=30°,∠A′DC=90°,然后在Rt△A′DC中利用含30度的直角三角形三边的关系得A′D=![]() CA′=1,CD=
CA′=1,CD=![]() A′D=
A′D=![]() ,再利用三角形面积公式求解.
,再利用三角形面积公式求解.
在Rt△ACB=90°,∵∠B=30°,
∴∠A=60°,
∵△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,
∴CA=CA′=2,∠CA′B′=∠A=60°,
∴△CAA′为等边三角形,
∴∠ACA′=60°,
∴∠BCA′=30°,
∴∠A′DC=90°,
在Rt△A′DC中,∵∠A′CD=30°,
∴A′D=![]() CA′=1,CD=
CA′=1,CD=![]() A′D=
A′D=![]() ,
,
∴△A′CD的面积=![]() ×1×
×1×![]() =
=![]() .
.
故选:A.

练习册系列答案
相关题目
【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
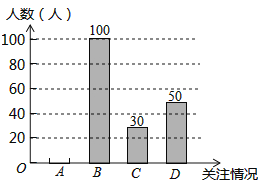
(1)根据上述统计表可得此次采访的人数为 人;m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约 人.