题目内容
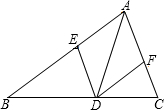
如图所示，点E在△ABC外部，点D在BC边上，DE交AC于F，若∠1=∠2，∠E=∠C，AE=AC，则（ ）
| A．△ABC≌△AFE | B．△AFE≌△ADC | C．△AFE≌△DFC | D．△ABC≌△ADE |
∵∠1=∠2，
∴∠1+∠DAC=∠2+∠DAC，即∠BAC=∠DAE，
在△ABC和△ADE中，
∵
，
∴△ABC≌△ADE（ASA）．
故选D．
∴∠1+∠DAC=∠2+∠DAC，即∠BAC=∠DAE，
在△ABC和△ADE中，
∵
|
∴△ABC≌△ADE（ASA）．
故选D．
练习册系列答案
名师点拨卷系列答案
相关题目
