��Ŀ����
����Ŀ����ͼ����֪![]() ��
��![]() �ı�
�ı�![]() ����һ����
����һ����![]() ���Ӿ���
���Ӿ���![]() ��
��![]() �ĵ�
�ĵ�![]() �����������߶�
�����������߶�![]() ������
������![]() �˶����ٶ�Ϊ
�˶����ٶ�Ϊ![]() ������
������![]() �ӵ�
�ӵ�![]() ������������
������������![]() �˶����ٶ�Ϊ
�˶����ٶ�Ϊ![]() ��
��![]() ��
��![]() ͬʱ������ͬʱ����
ͬʱ������ͬʱ����![]() ���ŵ�
���ŵ�![]() ��
��![]() ����ÿ��5�����ٶ�˳ʱ����ת�����˶�ʱ����
����ÿ��5�����ٶ�˳ʱ����ת�����˶�ʱ����![]() ��
��
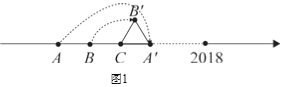
��1������![]() ��
��![]() ���˶�ʱ��
���˶�ʱ��![]()
![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2������![]() ���߶�
���߶�![]() ���˶�ʱ��
���˶�ʱ��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ����ʱ����
����ʱ����![]() ��
��![]() �Ľ�ƽ�������������˵�����ɣ�
�Ľ�ƽ�������������˵�����ɣ�
��3��������![]() ���Ƿ����
���Ƿ����![]() ��
��![]() ���
���![]() �������ڣ������t��ֵ�������ʱ
�������ڣ������t��ֵ�������ʱ![]() �Ķ������������ڣ���˵�����ɣ�
�Ķ������������ڣ���˵�����ɣ�

���𰸡���1����18-2t������2��6���ǣ����ɼ���⣻��3�����ڣ�t=16����BOC=20���t=20����BOC=40�㣮
��������
��1����������ȷ����PM=2t���Ӷ��������ɵó����ۣ�
��2���������ȸ���OP=OQ�����������t=6�����������AOC=30�㣬���ɵó����ۣ�
��3�����������P��Q����ǰ���2cm��������2cm�������������������⣬���ɵó����ۣ�
�⣺��1������P��MO���˶�ʱ�����˶�֪��PM=2t��
��OM=18cm��
��PO=OM-PM=��18-2t��cm��
�ʴ�Ϊ����18-2t����
��2���ɣ�1��֪��OP=18-2t��
��OP=OQʱ������18-2t=t��
��t=6
��t=6ʱ����ʹOP=OQ��
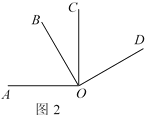
������OC���ŵ�O��OA����ÿ��5����ٶ�˳ʱ����ת��
���AOC=5���6=30�㣬
�ߡ�AOB=60�㣬
���BOC=��AOB-��AOC=30��=��AOC��
������OC�ǡ�AOB�Ľ�ƽ���ߣ�
��3������������
��P��Q����ǰ���2cmʱ��
OQ-OP=2
��t-��2t-18��=2
��������̣���t=16��
���AOC=5���16=80��
���BOC=80��-60��=20�㣬
��P��Q���������2cmʱ��OP-OQ=2
�ࣨ2t-18��-t=2
�ⷽ�̵�t=20��
���AOC=5���20=100��
���BOC=100��-60��=40�㣬
�ۺ�����t=16����BOC=20���t=20����BOC=40�㣮