题目内容
【题目】规律发现:
在数轴上
(1)点M表示的数是2,点N表示的数是8,则线段MN的中点P表示的数为______;
(2)点M表示的数是﹣3,点N表示的数是7,则线段MN的中点P表示的数为_____;发现:点M表示的数是a,点N表示的数是b,则线段MN的中点P表示的数为______.
直接运用:
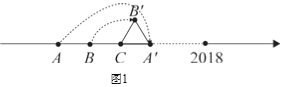
将数轴按如图1所示,从点A开始折出一个等边三角形A'B'C,设点A表示的数为x﹣3,点B表示的数为2x+1,C表示的数为x﹣1,则x值为_____,若将△A'B'C从图中位置向右滚动,则数2018对应的点将与△A'B'C的顶点_______重合.
类比迁移:
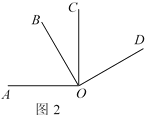
如图2:OA⊥OC,OB⊥OD,∠COD=60°,若射线OA绕O点以每秒15°的速度顺时针旋转,射线OB绕O点以每秒10°的速度顺时针旋转,射线OC绕O点以每秒5°的速度逆时针旋转,三线同时旋转,当一条射线与射线OD重合时,三条射线同时停止运动.
①求射线OC和射线OB相遇时,∠AOB的度数;
②运动几秒时,射线OA是∠BOC的平分线?
【答案】规律发现:(1)5;(2)2,![]() ;直接运用:-3,C;类比迁移:①∠AOB=50°;②运动6秒时,OA是∠BOC的平分线.
;直接运用:-3,C;类比迁移:①∠AOB=50°;②运动6秒时,OA是∠BOC的平分线.
【解析】
(1)规律发现:根据线段的中点的定义解答即可;
(2)直接运用:根据等边三角形ABC边长相等,求出x的值,再利用数字2018对应的点与![]() 的距离,求得C从出发到2018点滚动的周数,即可得出答案;
的距离,求得C从出发到2018点滚动的周数,即可得出答案;
类比迁移:①设x秒后射线OC和射线OB相遇,可得方程![]() ,解方程求出t的值,即可求出
,解方程求出t的值,即可求出![]() 的度数;
的度数;
②设y秒时,射线OA是![]() 的平分线,可得方程
的平分线,可得方程![]() ,解方程即可解答.
,解方程即可解答.
解:(1)点M表示的数是2,点N表示的数是8,则线段MN的中点P表示的数为![]() ,
,
故答案为:5;
(2)点M表示的数是3,点N表示的数是7,则线段MN的中点P表示的数为![]() ,
,
故答案为:2;
发现:点M表示的数是a,点N表示的数是b,则线段MN的中点P表示的数为![]() ;
;
故答案为:![]() ;
;
直接运用:
∵将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x3,点B表示的数为2x+1,点C表示的数为4,
∴4(2x+1)=2x+1(x3);
∴3x=9,
x=3.
故A表示的数为:x3=33=6,
点B表示的数为:2x+1=2×(3)+1=5,
即等边三角形ABC边长为1,
数字2018对应的点与4的距离为:2018+4=2022,
∵2022÷3=674,C从出发到2018点滚动674周,
∴数字2018对应的点将与△ABC的顶点C重合;
类比迁移:
① ∵OB⊥OD
∴∠DOB=90°
∵∠COD=60°
∴∠BOC=∠DOB- ∠COD =30°
设运动t秒时射线OB和射线OC相遇
根据题意得:5t+10t=30
解之得:t=2
此时∠AOB=60°+10°×2-15°×2=50°;
②设运动x秒时OA是∠BOC的平分线
15x+5x﹣90=60+10x﹣15x
解得x=6.
故运动6秒时,OA是∠BOC的平分线.