题目内容
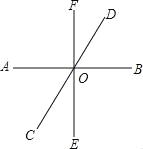
【题目】如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【答案】(1)∠COE的邻补角为∠COF和∠EOD;(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;(3)∠FOC=150°.
【解析】试题分析:(1)根据邻补角的定义(两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角)可得,∠COE的邻补角有∠COF和∠EOD两个角;(2)根据对顶角的定义(一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点)可得,∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;(3)由∠BOF=90°可得:AB⊥EF,所以∠AOF=90°,由∠AOC=∠BOD可得:∠AOC =60°,由∠FOC=∠AOF+∠AOC即可求出∠FOC的度数;
试题解析:
(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目