题目内容
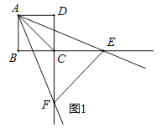
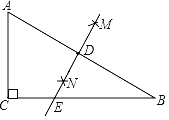
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点.以
的中点.以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() .
.
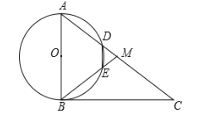
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半得AM=BM,进而得∠A=∠ABM,再根据圆内接四边形的性质得∠MDE=∠ABM,进而得∠A=∠MDE,据此可得答案.
(2)连接BD,由三角形面积求出BD,进而由勾股定理求得AD,再由△MDE∽△MAB求得DE.
解:(1)证明:∵BC与![]() 相切于点B,∴∠ABC=90°,
相切于点B,∴∠ABC=90°,
∵点M是AC的中点,∴BM=AM=CM,
∴∠MAB=∠MBA,
∵四边形ABED是![]() 的内接四边形,
的内接四边形,
∴∠ADE+∠ABE=180°,
∵∠MDE+∠ADE=180°,
∴∠MDE=∠ABE,
∴∠MDE=∠MAB.
∴DE∥AB.
(2)连接BD,如下图所示:
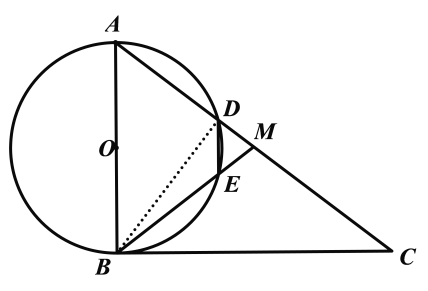
∵AB=6,BC=8,∠ABC=90°,
∴由勾股定理求得AC=10,
∵AB是![]() 的直径,
的直径,
∴∠ADB=90°,
∵AB×BC=AC×BD
∴![]() ,
,
∴![]() ,
,
∴DM=AM-AD=5-3.6=1.4,
∵DE∥AB,
∴△MDE∽△MAB,
∴![]() ,代入数据:
,代入数据:![]()
解得![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某数学兴趣小组的同学在研究函数![]() 的图象时,先对函数
的图象时,先对函数![]() 的图象进行了如下探索.
的图象进行了如下探索.
![]() ①列表:列出
①列表:列出![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
②描点:根据表中数据描点如图所示;
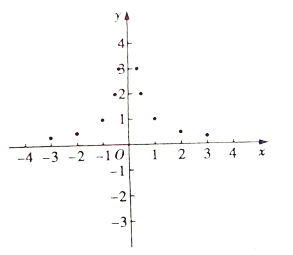
③连线:请在图中画出函数![]() 的图象;
的图象;
④观察图象,写出两条关于该函数的性质.
![]() 根据以上探究结果,完成下列问题:
根据以上探究结果,完成下列问题:
①函数![]() 中,自变量
中,自变量![]() 的取值范围为 ;
的取值范围为 ;
②函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
③写出两条关于函数![]() 的性质;
的性质;
④直接写出不等式![]() 的解集.
的解集.