Question

【题目】如图，Rt△AOB的顶点O与原点重合，直角顶点A在x轴上，顶点B的坐标为（4，3），直线y＝﹣x+4与x轴、y轴分别交于点D、E，交OB于点F．

（1）求点D、E两点的坐标及DE的长；

（2）写出图中的全等三角形及理由．

Answer 1

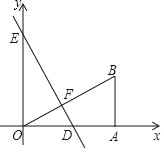
【答案】(1) 点D（3，0），点E（0，4），DE＝5；(2) △EOD≌△OAB，理由见解析.

【解析】

（1）根据题意和一次函数的性质、勾股定理可以求得点D、E两点的坐标及DE的长；

（2）根据题意和图形，写出两个三角形全等，然后根据全等三角形的判定证明即可解答本题．

解：（1）∵直线y＝﹣x+4与x轴、y轴分别交于点D、E，

∴当y＝0时，x＝3，当x＝0时，y＝4，

∴点D（3，0），点E（0，4），

∴OD＝3，OE＝4，

∵∠DOE＝90°，

∴DE＝=＝5，

即点D（3，0），点E（0，4），DE＝5；

（2）△EOD≌△OAB，

理由：∵由（1）点D（3，0），点E（0，4），∠EOD＝90°，

∴OE＝4，OD＝3，

∵Rt△AOB的顶点O与原点重合，直角顶点A在x轴上，顶点B的坐标为（4，3），

∴AO＝4，AB＝3，∠OAB＝90°，

∴OE＝AO，OD＝AB，∠EOD＝∠OAB，

在△EOD和△OAB中，

，

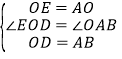∴△EOD≌△OAB（SAS）