题目内容

【题目】如图，已知∠AOB＝90°，∠BOC比∠AOC大30°，OD是∠AOB的平分线，求∠COD的度数．

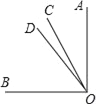
【答案】15°

【解析】

设∠AOC=x°，则∠BOC=（x+30）°，由∠AOC+∠BOC=∠AOB=90°，可求∠AOC=30°，∠BOC=60°，又因为OD是∠AOB的平分线，可得∠AOD=45°，所以∠COD=∠AOD﹣∠AOC=15°．

设∠AOC=x°，则∠BOC=（x+30）°．

∵∠AOC+∠BOC=∠AOB=90°，即：x+（x+30）=90°，∴x=30°，x+30=60°，∴∠AOC=30°，∠BOC=60°．

∵OD是∠AOB的平分线，∴∠AOD∠AOB90°=45°，∴∠COD=∠AOD﹣∠AOC=15°．

练习册系列答案
相关题目

【题目】课题学习：设计概率模拟实验． 在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是 ．”小海、小东、小英分别设计了下列三个模拟实验：
小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；
小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．

根据以上材料回答问题：
小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．

【题目】如图，Rt△AOB的顶点O与原点重合，直角顶点A在x轴上，顶点B的坐标为（4，3），直线y＝﹣x+4与x轴、y轴分别交于点D、E，交OB于点F．

（1）求点D、E两点的坐标及DE的长；

（2）写出图中的全等三角形及理由．

【题目】已知：如同，△ABC内接于⊙O，且半径OC⊥AB，点D在半径OB的延长线上，且∠A=∠BCD=30°，AC=2，则由 ，线段CD和线段BD所围成图形的阴影部分的面积为 ．

【题目】某地雪灾发生之后，灾区急需帐篷。某车间的甲、乙两名工人分别同时生产同种帐篷上的同种零件，他们一天生产零件y（个）与生产时间t（时）的函数关系如图所示。

①甲、乙中______先完成一天的生产任务；在生产过程中，______因机器故障停止生产______小时。

②当t＝______时，甲、乙生产的零件个数相等。

【题目】如图，四边形ABCD内接于⊙O，AB是⊙O的直径，点P在CA的延长线上，∠CAD=45°．
（Ⅰ）若AB=4，求 的长；
（Ⅱ）若 = ，AD=AP，求证：PD是⊙O的切线．

【题目】我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下，它们会全等?

（1）阅读与证明：

对于这两个三角形均为直角三角形，显然它们全等.

对于这两个三角形均为钝角三角形，可证它们全等（证明略）.

对于这两个三角形均为锐角三角形，它们也全等，可证明如下：

已知：△ABC、△A1B1C1均为锐角三角形，AB＝A1B1，BC＝B1C1，∠C＝∠C1.

求证：△ABC≌△A1B1C1. （请你将下列证明过程补充完整）

证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1.

则∠BDC＝∠B1D1C1＝90°，

∵BC＝B1C1，∠C＝∠C1，

∴△BCD≌△B1C1D1，

∴BD＝B1D1.

______________________________。

（2）归纳与叙述：

由（1）可得到一个正确结论，请你写出这个结论.

【题目】如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G，AE=2，则EG的长是 ．

【题目】已知，点O是直线AB上一点，OC、OD为从点O引出的两条射线，∠BOD=30°，∠COD=∠AOC．

（1）如图①，求∠AOC的度数；

（2）如图②，在∠AOD的内部作∠MON=90°，请直接写出∠AON与∠COM之间的数量关系　 　；

（3）在（2）的条件下，若OM为∠BOC的角平分线，试说明∠AON=∠CON．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网