题目内容
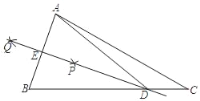
【题目】如图,直线![]() 和
和![]() 相交于点
相交于点![]() ,
,![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交射线
的垂线交射线![]() 于点
于点![]() .
.
(1)确定点![]() 的位置,在线段
的位置,在线段![]() 上任取一点
上任取一点![]() ,根据题意,补全图形;
,根据题意,补全图形;
(2)设![]() cm,
cm,![]() cm,探究函数
cm,探究函数![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
①通过取点、画图、测量,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
(要求:补全表格,相关数值保留一位小数)
②)建立平面直角坐标系![]() ,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;

③结合画出的函数图象,解决问题:当![]() 为
为![]() 斜边
斜边![]() 上的中线时,
上的中线时,![]() 的长度约为_____cm(结果保留一位小数).
的长度约为_____cm(结果保留一位小数).
【答案】(1)见解析;(2)①见解析;②见解析;③![]()
【解析】
(1)根据题意直接画出图形;
(2)①先求出BC,AC,进而求出BG,CG,再判断出△DEF∽△CDG,进而得出DF=3![]() EF,再判断出DF=3AF,利用AD=4求出AF,进而求出AE,即可得出结论;②先描点,再连线,即可得出结论;③先判断出AD=AC,即可得出结论.
EF,再判断出DF=3AF,利用AD=4求出AF,进而求出AE,即可得出结论;②先描点,再连线,即可得出结论;③先判断出AD=AC,即可得出结论.
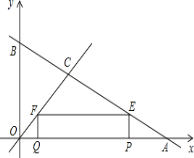
(1)如图1所示,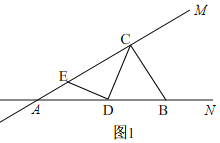
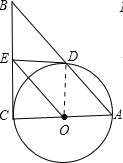
(2)①如图2,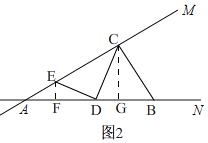
在Rt△ABC中,∠BAC=30°,AB=6,
∴BC=3,AC=3![]() ,
,
过点C作CG⊥AB于G,
在Rt△BCG中,BG=![]() BC=
BC=![]() ,CG=
,CG=![]() ,
,
∵AB=6,AD=4,
∴DG=AB-AD-BG=6-4-![]() =
=![]() ,
,
过点E作EF⊥AB于F,
∴∠DFE=∠CGD=90°.
∴∠DCG+∠CDG=90°,
∵DE⊥CD,
∴∠CDG+∠EDF=90°,
∴∠DCG=∠EDF,
∵∠EFD=∠DGC=90°,
∴△DEF∽△CDG,
∴![]()
∴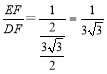 ,
,
∴DF=3![]() EF,
EF,
在Rt△AEF中,AF=![]() EF,AE=
EF,AE=![]() AF,
AF,
∴DF=3AF,
∴AD=AF+DF=4AF=4,
∴AF=1,
∴AE=![]() ,
,
∴y=CE=AC-AE=3![]() -
-![]() =
=![]() ≈4.0,
≈4.0,
故答案为:4.0;
②函数图象如图3所示,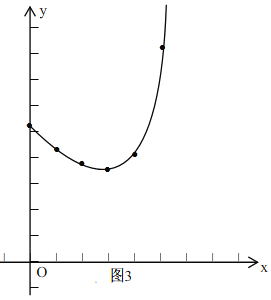
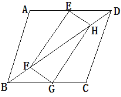
③如图4,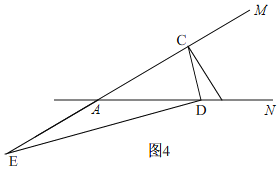
∵AD是Rt△CDE的斜边的中线,
∴AD=![]() CE=AC,
CE=AC,
由(2)知,AC=3![]() ,
,
∴AD=3![]() ≈5.2,
≈5.2,
故答案为:5.2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案