题目内容
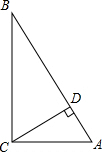
在三角形ABC中,∠C=90°,∠A,∠B,∠C对应的边分别是a,b,c,其中a-b=2 ,CD⊥AB于D,BD-AD=2
,CD⊥AB于D,BD-AD=2 ,求△ABC三边的长.
,求△ABC三边的长.
 解:设AB=c,CD=h
解:设AB=c,CD=hBD=a×sinA=a×
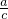 ,AD=b×cosA=b×
,AD=b×cosA=b× ,
,BD-AD=
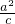 -
-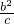 =
= =2
=2
a-b=2

a+b=(
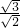 )×c
)×c 两边同时平方得:c2+2ab=
 c2
c2 ∴2ab=
 c2,
c2,∵
 ab=
ab= ch,
ch,∴ab=ch=
 c2,
c2,∴4h=c
a2+b2-2ab=8
c2-2ch=8
c2-
 c2=8
c2=8 c=4
a=
 +
+ b=
b= -
-
分析:设出斜边长和斜边上的高,利用锐角三角函数表示出a与b的和,再利用已知条件中的两边之差求得a和b的值即可.
点评:本题考查了勾股定理的知识,解题的关键是利用锐角三角函数值表示出两直角边的和,然后利用已知条件求得两直角边的值.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
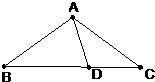 22、如图,在三角形ABC中,AB=AC=BD,AD=CD,则∠B=
22、如图,在三角形ABC中,AB=AC=BD,AD=CD,则∠B=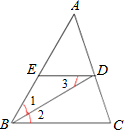 20、如图,在三角形ABC中,BD平分∠ABC,∠1=∠3,求证:∠ADE=∠C.
20、如图,在三角形ABC中,BD平分∠ABC,∠1=∠3,求证:∠ADE=∠C.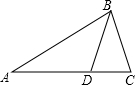 如图,在三角形ABC中,若AB=AC,BD=BC,若∠ABD=30°,则∠A的大小是
如图,在三角形ABC中,若AB=AC,BD=BC,若∠ABD=30°,则∠A的大小是