题目内容
【题目】我们把a、b两个数中较小的数记作min{a，b}，直线y=kx﹣k﹣2（k＜0）与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点，则k的取值为 ．
【答案】2﹣2
或
或﹣1．
【解析】
试题分析：根据题意，x2﹣1＜﹣x+1，即x2+x﹣2＜0，
解得：﹣2＜x＜1，
故当﹣2＜x＜1时，y=x2﹣1；
当x≤﹣2或x≥1时，y=﹣x+1；
函数图象如下：
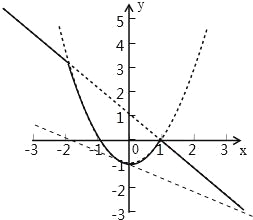
由图象可知，∵直线y=kx﹣k﹣2（k＜0）与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点，且k＜0，
①直线y=kx﹣k﹣2经过点（﹣2，3）时，3=﹣2k﹣k﹣2，k=
，此时直线y=x
，与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点．
②直线y=kx﹣k﹣2与函数y=x2﹣1相切时，由
消去y得x2﹣kx+k+1=0，∵△=0，k＜0，
∴k2﹣4k﹣4=0，
∴k=2﹣2
（或2+2舍弃），此时直线y=（2﹣2）x﹣4+2与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点．
③直线y=kx﹣k﹣2和直线y=﹣x+1平行，k=﹣1，直线为y=﹣x﹣1与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点．
综上，k=2﹣2或-
或﹣1．
故答案为：2﹣2或-或﹣1．
练习册系列答案
相关题目
