题目内容
【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( ) 
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5
【答案】B
【解析】解:如图,连接OA,作OM⊥AB于M, ∵⊙O的直径为10,
∴半径为5,
∴OM的最大值为5,
∵OM⊥AB与M,
∴AM=BM,
∵AB=6,
∴AM=3,
在Rt△AOM中,OM= ![]() =
= ![]() =
= ![]() =4;
=4;
此时OM最短,
当OM是半径时最长,OM=5.
所以OM长的取值范围是4≤OM≤5.
故选B.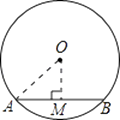
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校在艺术节选拔节目过程中,从备选的“街舞”、“爵士”、“民族”、“拉丁”四种类型舞蹈中,选择一种学生最喜爱的舞蹈,为此,随机调查了本校的部分学生,并将调查结果绘制成如下统计图表(每位学生只选择一种类型),根据统计图表的信息,解答下列问题:
类型 | 民族 | 拉丁 | 爵士 | 街舞 |
据点百分比 | a | 30% | b | 15% |

(1)本次抽样调查的学生人数及a、b的值.
(2)将条形统计图补充完整.
(3)若该校共有1500名学生,试估计全校喜欢“拉丁舞蹈”的学生人数.