题目内容
【题目】已知方程
，
（1）求证：方程一定有两个不相等的实数根；
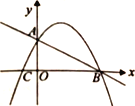
（2）
取何值时，方程二根中一个比3大，一个比3小。（可用数形结合来解）
（3）取何值时方程的两个根异号且负的实数根的绝对值大.
【答案】（1）见解析；（2）a＞1；（3）a＜0．
【解析】
（1）求出△的值，再判断即可；
（2）由题意得
，即
，再根据根与系数关系解答即可；
（3）由题意可得x1+x2＜0，x1x2＜0，，根据根与系数关系即可解答．
解：（1）方程x2-2ax+a=4，可化为：x2-2ax+a-4=0，
∴△=4a2-4（a-4）=4(a
)2+15＞0，故方程一定有两个不相等的实数根；
（2）∵方程二根中一个比3大，一个比3小，
∴
∵x1+x2=2a，x1x2=a-4，
∴（a-4）-3×2a +9＜0，
解得：a＞1，
∴a＞1时，方程二根中一个比3大，一个比3小；
（3）若方程有两根相异，并且负根的绝对值较大，则可得：x1+x2=2a＜0，x1x2=a-4＜0，解得：a＜0．
故答案为：（1）见解析；（2）a＞1；（3）a＜0．
练习册系列答案
阅读快车系列答案
相关题目
