题目内容
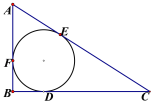
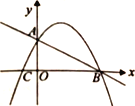
【题目】如图，直线
交坐标轴于A、B两点，直线AC⊥AB交x轴于点C，抛物线恰好过点A、B、C.
（1）求抛物线的表达式.
（2）当点M在线段AB上方的曲线上移动时，求四边形AOBM的面积的最大值.
【答案】（1）
；（2）
；
【解析】
（1）由直线解析式可求出A、B两点坐标，由AC⊥AB，可证明ΔAOC∽ΔBOA，根据相似三角形的性质可求出OC的长，即可得C点坐标，利用待定系数法即可得出抛物线的解析式；（2）过M点作MN⊥x轴，交直线AB于D点，设M点的横坐标为a，可得出M点和D点坐标，进而求出MD的长，可得△ABM的面积，根据S四边形AOBM=S△AOB+S△ABM可得关于a的二次函数，根据二次函数的性质即可求出四边形AOBM面积的最大值；
（1）∵直线
交坐标轴A、B两点，
∴A（0，2）、B（4，0），
∴OA=2，OB=4，
∵AC⊥AB，OA⊥BC，
∴∠AOB=∠AOC=90°，∠OAC+∠OAB=90°，∠OAC+∠OCA=90°，
∴∠OCA=∠OAB，
∴ΔAOC∽ΔBOA
∴
，
解得：OC=1
∴C（-1，0）
设抛物线的表达式为：
，得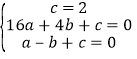
，
解得
，
∴抛物线的表达式为：
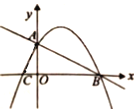
（2）过M点作MN⊥x轴，交直线AB于D点
设M点的横坐标为a，则M（a，
）、D（a，
）
∴
∴
∴
当a=2时，
的值最大，则
练习册系列答案
相关题目
