Question

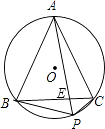
【题目】如图，两个同心圆的半径分别为4cm和5cm，大圆的一条弦AB与小圆相切，则弦AB的长为（ ）
A.6cm
B.4cm
C.3cm
D.8cm

Answer 1

【答案】A
【解析】解：如图，连接OC，AO，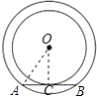
∵大圆的一条弦AB与小圆相切，
∴OC⊥AB，
∴AC=BC= AB，
∵OA=5cm，OC=4cm，
在Rt△AOC中，AC= =3cm，
∴AB=2AC=6（cm）．
故选A．
【考点精析】掌握切线的性质定理和圆与圆的位置关系是解答本题的根本，需要知道切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；两圆之间有五种位置关系：无公共点的，一圆在另一圆之外叫外离，在之内叫内含；有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；有两个公共点的叫相交．两圆圆心之间的距离叫做圆心距．两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r．