题目内容
已知a、b均为正数,且a+b=2,求W=| a2+4 |
| b2+1 |
分析:将b=2-a代入W=
+
,得到W的关于a的表达式,再利用勾股定理,将表达式转化为直角三角形两斜边AP、BP的和,利用勾股定理求和即可.
| a2+4 |
| b2+1 |
解答: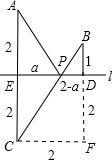 解:得W=
解:得W=
+
,(5分)
构造如下图形,其中ED=2,AE=2,BD=1,AE⊥l,BD⊥l,
P是ED上任意一点,点C是点A关于直线l的对称点,
设PE=a,则W=
+
=AP+BP,(5分)
当B、P、C三点共线时,W的值最小,此时由勾股定理可求得
+
的最小值为
.(5分)
 解:得W=
解:得W=| a2+22 |
| (2-a)2+12 |
构造如下图形,其中ED=2,AE=2,BD=1,AE⊥l,BD⊥l,
P是ED上任意一点,点C是点A关于直线l的对称点,
设PE=a,则W=
| a2+22 |
| (2-a)2+12 |
当B、P、C三点共线时,W的值最小,此时由勾股定理可求得
| a2+4 |
| b2+1 |
| 13 |
点评:此题考查了轴对称---最短路径问题,将表达式转化为勾股定理,体现了数形结合在解题中的作用.

练习册系列答案
相关题目