题目内容
(1)设a、b、c、d为正实数,a<b,c<d,bc>ad,有一个三角形的三边长分别为| a2+c2 |
| b2+d2 |
| (b-a)2+(d-c)2 |
(2)已知a,b均为正数,且a+b=2,求U=
| a2+4 |
| b2+1 |
分析:(1)显然不能用面积公式求三角形面积,
的几何意义是以a、c为直角边的直角三角形的斜边,从构造图形人手,将复杂的根式计算转化为几何问题加以解决;
(2)用代数的方法求U的最小值较繁,运用对称分析,借助图形求U的最小值.
| a2+c2 |
(2)用代数的方法求U的最小值较繁,运用对称分析,借助图形求U的最小值.
解答:解:如图1,作长方形ABCD,使AB=b-a,AD=c,
延长DA至E,使DE=d,延长DC至F,使DF=b,连接EF、FB,
则BF=
,EF=
,BE=
,
从而可知△BEF就是题设的三角形;
而S△BEF=S长方形ABCD+S△BCF+S△ABE-S△DEF
=(b-a)c+
ac+
(d-c)(b-a)-
bd
=
(bc-ad);
(2)将b=2-a代入U=
+
中,得U=
+
,
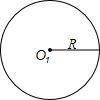
构造图形(如图2),
可得U的最小值为A′B=
=
.
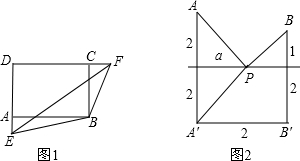
延长DA至E,使DE=d,延长DC至F,使DF=b,连接EF、FB,
则BF=
| a2+c2 |
| b2+d2 |
| (b-a)2+(d-c)2 |
从而可知△BEF就是题设的三角形;
而S△BEF=S长方形ABCD+S△BCF+S△ABE-S△DEF
=(b-a)c+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
(2)将b=2-a代入U=
| a2+4 |
| b2+1 |
| a2+22 |
| (2-a)2+12 |
构造图形(如图2),
可得U的最小值为A′B=
| A′B′2+BB′2 |
| 13 |

点评:本题考查了二次根式在计算图形面积,勾股定理中的运用.关键是根据题意,构造图形求解.

练习册系列答案
相关题目
八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设同学人数为x人,下列各项能准确的求出同学人数与种植的树木的数量的是( )
| A、7x+9-9(x-1)>0 | |||||
| B、7x+9-9(x-1)<8 | |||||
C、
| |||||
D、
|
 已知⊙O1的半径为R,周长为C.
已知⊙O1的半径为R,周长为C. 如图,若反比例函数y=-
如图,若反比例函数y=-