题目内容
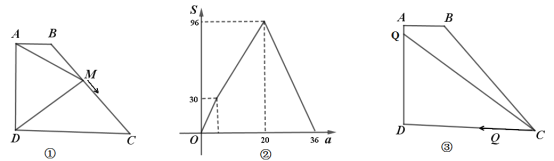
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计),第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车,小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林,离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
(1)求第一班车从入口处到达塔林的时间.
(2)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变).
(3)若小聪在8:30至8:50之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过3分钟的概率是多少?

【答案】(1)10;(2)7;(3)![]() .
.
【解析】
(1)根据题意设y=kx+b,运用待定系数法求解并把y=1500代入即可得出答案;
(2)由题意设小聪坐上了第n班车,30-25+10(n-1)≥40,解得n≥4.5,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可;
(3)根据题意求出小聪等车时间不超过3分钟的时间长度,代入概率计算公式,即可得出答案.
解:(1)由题意可设函数表达式为:y=kx+b(k≠0),
把(20,0),(38,2700)代入y=kx+b,得![]() ,解得
,解得![]() ,
,
∴第一班车离入口处的路程y(米)与时间x(分)的函数表达为y=150x-3000(20≤x≤38);
把y=1500代入y=150x-3000,解得x=30,
30-20=10(分),
∴第一班车从入口处到达塔林所需时间10分钟.
(2)设小聪坐上了第n班车,则30-25+10(n-1)≥40,解得n≥4.5,
∴小聪坐上了第5班车,
即等车的时间为5分钟,坐班车所需时间为:1200÷150=8(分),
步行所需时间:1200÷(1500÷25)=20(分),
20-(8+5)=7(分),
∴比他在塔林游玩结束后立即步行到草甸提早了7分钟.
(3)由题意设小聪到达时间为y,
当y在8:37至8:40,或8:47至8:57时,共计6分钟,聪等车时间不超过3分钟,
又小聪在8:30至8:50之间到达发车站乘坐班车,故有其概率为:![]() .
.

【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 唱歌 | 35% |
B | 舞蹈 | a |
C | 朗诵 | 25% |
D | 器乐 | 30% |
请结合统计图表,回答下列问题: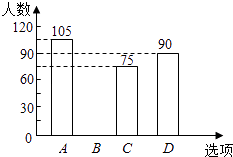
(1)本次调查的学生共人,a= , 并将条形统计图补充完整 ;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.