题目内容
【题目】已知A(m,n),且满足m-2+(n-2)2=0,过A作AB⊥y轴,垂足为B.
(1)求A点坐标；
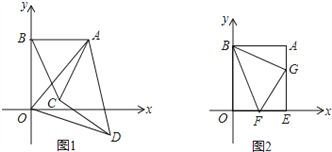
(2)如图1,分别以AB,AO为边作等边△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由；
(3)如图2,过A作AE⊥x轴,垂足为E,点F、G分别为线段OE、AE上的两个动点 (不与端点重合),满足∠FBG=45°,设OF=a,AG=b,FG=c,试探究
的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
【答案】（1）A（2，2）；（2）AC＝CD，AC⊥CD，理由见解析；（3）定值为0，
【解析】试题分析：（1）根据非负数的性质可得m、n的值；
（2）连接OC，由AB=BO知∠BAO=∠BOA=45°，由△ABC，△OAD为等边三角形知∠BAC=∠OAD=∠AOD=60°、OA=OD，继而由∠BAC-∠OAC=∠OAD-∠OAC得∠DAC=∠BAO=45°，根据OB=CB=2、∠OBC=30°知∠BOC=75°，∠AOC=∠BAO-∠BOA=30°，∠DOC=∠AOC=30°，证△OAC≌△ODC得AC=CD，再根据∠CAD=∠CDA=45°知∠ACD=90°，从而得AC⊥CD；
（3）在x轴负半轴取点M，使得OM=AG=b，连接BG，先证△BAG≌△BOM得∠OBM=∠ABG、BM=BG，结合∠FBG=45°知∠ABG+∠OBF=45°，从而得∠OBM+∠OBF=45°，∠MBF=∠GBF，再证△MBF≌△GBF得MF=FG，即a+b=c，代入原式可得答案．
试题解析：（1）由题得m=2，n=2，
∴A（2，2）；
（2）如图1，连结OC，
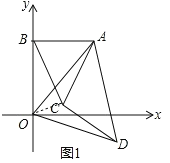
由（1）得AB=BO=2，
∴△ABO为等腰直角三角形，
∴∠BAO=∠BOA=45°，
∵△ABC，△OAD为等边三角形，
∴∠BAC=∠OAD=∠AOD=60°，OA=OD
∴∠BAC-∠OAC=∠OAD-∠OAC
即∠DAC=∠BAO=45°
在△OBC中，OB=CB=2，∠OBC=30°，
∴∠BOC=75°，
∴∠AOC=∠BAO-∠BOA=30°，
∴∠DOC=∠AOC=30°，
在△OAC和△ODC中，
∵
，
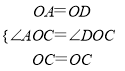∴△OAC≌△ODC，
∴AC=CD，
∴∠CAD=∠CDA=45°，
∴∠ACD=90°，
∴AC⊥CD；
（3）如图，在x轴负半轴取点M，使得OM=AG=b，连接BG，
在△BAG和△BOM中，
∵
，
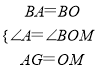∴△BAG≌△BOM
∴∠OBM=∠ABG，BM=BG
又∠FBG=45°
∴∠ABG+∠OBF=45°
∴∠OBM+∠OBF=45°
∴∠MBF=∠GBF
在△MBF和△GBF中，
∵
，
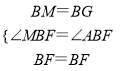∴△MBF≌△GBF
∴MF=FG
∴a+b=c代入原式=0．
