��Ŀ����
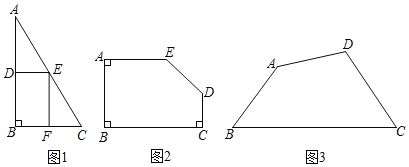
����Ŀ��С�����о�������ľ�����ϲó��������ľ�����ʱ���֣���ͼ1��![]() ��һ��ֱ����������״��ľ������
��һ��ֱ����������״��ľ������![]() ����
����![]() Ϊ�ڽDz�һ�����ε�DE��EF����λ��ʱ�����þ��ε�������
Ϊ�ڽDz�һ�����ε�DE��EF����λ��ʱ�����þ��ε�������![]() ��ľ�����ϵ���״�ı䣬����̽����
��ľ�����ϵ���״�ı䣬����̽����
![]() ��ͼ2������һ������ε�ľ������ABCDE��
��ͼ2������һ������ε�ľ������ABCDE��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ִ��вó�һ����
�ִ��вó�һ����![]() Ϊ�ڽ���������ľ��Σ���þ��ε����Ϊ______
Ϊ�ڽ���������ľ��Σ���þ��ε����Ϊ______![]() ��
��
![]() ��ͼ3������һ���ı��ε�ľ������ABCD��������
��ͼ3������һ���ı��ε�ľ������ABCD��������![]() ��
��![]() ��
��![]() ����
����![]() �����вó�����M��N�ڱ�BC����������ľ���PQMN����þ��ε����Ϊ______
�����вó�����M��N�ڱ�BC����������ľ���PQMN����þ��ε����Ϊ______![]() ��
��
���𰸡�400�� 486��
��������
��1����ͼ2�У��ӳ�AE��CD���ӳ�����F�����ı���ABCF�Ǿ��Σ�������ת��Ϊ�������ڽӾ��μ��ɽ�����⣮
��2���������κ��������ö��κ��������ʽ�����⼴�ɣ�
�⣺��1����ͼ2�У��ӳ�AE��CD���ӳ�����F�����ı���ABCF�Ǿ��Σ�
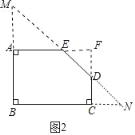
��AF��BC��30cm��AB��CF��20cm��
��AE��20cm��CD��10cm��
��EF��DF��10cm��
�ߡ�F��90����
���AEM����FED����FDE����CDN��45����
��AM��AE��20cm��CD��CN��10cm��
��BM��40cm��BN��40cm��
���BMN���ڽӾ��ε���������ֵ��20��20��400��cm2����
��2����ͼ3�У�
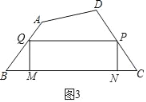
���ı���MNPQ�Ǿ��Σ�tanB��tanC��![]() ��
��
����Լ���QM��PN��4k��BM��CN��3k��
��MN��54��6 k��
��S����MNPQ��4k��54��6k������24��k��![]() ��2+486��
��2+486��
�ߩ�24��0��
��k��![]() ʱ������MNPQ�����������ֵΪ486��
ʱ������MNPQ�����������ֵΪ486��
��ʱBQ��PC��5k��![]() ���������⣬
���������⣬
�����MNPQ����������ֵΪ486cm2��
�ʴ�Ϊ400��486��