题目内容
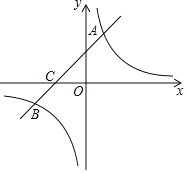
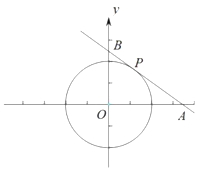
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画![]() ,P是
,P是![]() 上一动点,且P在第一象限内,过点P作
上一动点,且P在第一象限内,过点P作![]() 的切线与x轴相交于点A,与y轴相交于点B.在
的切线与x轴相交于点A,与y轴相交于点B.在![]() 上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.
上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.
【答案】![]() 或
或![]()
【解析】
分两种情况:OPAQ为平行四边形时,得出OQ⊥OP,AQ⊥AB,进而得出△POQ是等腰直角三角形,得出∠AOQ=∠AOP=45°,即可得出Q点坐标;OAPQ为平行四边形时,同理也可得出Q点坐标.
分两种情况:
如图OPAQ为平行四边形,

∴PO∥QA,OQ∥PA;
∵AB⊥OP,
∴OQ⊥OP,AQ⊥AB,
∴∠POQ=90°,
∵OP=OQ,
∴△POQ是等腰直角三角形,
∴OA是∠POQ的平分线且是边PQ上的中垂线,
∴∠AOQ=∠AOP=45°,
∴∠BOP=45°,
设P(x,x)、Q(x,-x)(x>0),
∵OP=2
∴![]() 解得
解得![]()
∴Q点坐标是![]()
②如图示OAPQ为平行四边形,
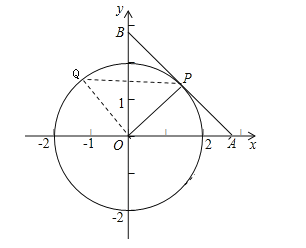
同理可得Q点坐标是![]()

练习册系列答案
相关题目