题目内容
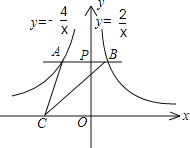
【题目】如图，在平面直角坐标系中，一次函数
的图象与反比例函数
的图象相交于第一、三象限内的
两点，与
轴交于点
.
⑴求该反比例函数和一次函数的解析式；
⑵在
轴上找一点
使
最大，求的最大值及点的坐标；
⑶直接写出当
时，的取值范围.
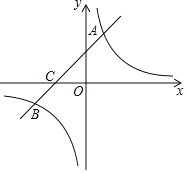
【答案】⑴
，
；⑵
的最大值为
，
；⑶
或
.
【解析】
（1）利用待定系数法，即可得到反比例函数和一次函数的解析式；
（2）根据一次函数y1=x+2，求得与y轴的交点P，此交点即为所求；
（3）根据AB两点的横坐标及直线与双曲线的位置关系求x的取值范围．
⑴.∵
在反比例函数
上
∴
∴反比例函数的解析式为
把
代入可求得
∴
.
把
代入
为
解得
.
∴一次函数的解析式为.
⑵的最大值就是直线
与两坐标轴交点间的距离.
设直线与
轴的交点为
.
令
，则
，解得
，∴
令
，则
，，∴
∴
,
∴的最大值为
.
⑶根据图象的位置和图象交点的坐标可知：
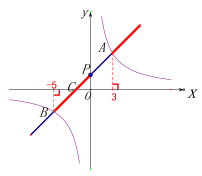
当
时
的取值范围为;或.
练习册系列答案
轻松课堂标准练系列答案
相关题目
