题目内容
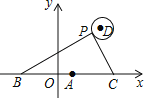
【题目】如图,在△ABC中,∠B=45°,AC=5,cosC=![]() ,AD是BC边上的高线.
,AD是BC边上的高线.
(1)求AD的长;
(2)求△ABC的面积.
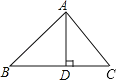
【答案】(1)AD=4;(2)S△ABC=14.
【解析】
(1)由高的定义可得出∠ADC=∠ADB=90°,在Rt△ACD中,由AC的长及cosC的值可求出CD的长,再利用勾股定理即可求出AD的长;
(2)由∠B,∠ADB的度数可求出∠BAD的度数,即可得出∠B=∠BAD,利用等角对等边可得出BD的长,再利用三角形的面积公式即可求出△ABC的面积.
解:(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°.
在Rt△ACD中,AC=5,cosC=![]() ,
,
∴CD=ACcosC=3,
∴AD=![]() =4.
=4.
(2)∵∠B=45°,∠ADB=90°,
∴∠BAD=90°﹣∠B=45°,
∴∠B=∠BAD,
∴BD=AD=4,
∴S△ABC=![]() ADBC=
ADBC=![]() ×4×(4+3)=14.
×4×(4+3)=14.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
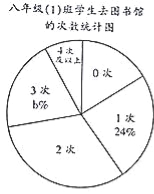
【题目】达州市图书馆今年4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图不完整的统计图表.
八年级(1)班学生去新图书馆的次数统计表
去图书馆的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 8 | 12 | a | 10 | 4 |
请你根据统计图表中的信息,解答下列问题:
(1)填空:a= ,b= ;
(2)求扇形统计图中“0次”的扇形所占圆心角的度数;
(3)从全班去过该图书馆的同学中随机抽取1人,谈谈对新图书馆的印象和感受.求恰好抽中去过“4次及以上”的同学的概率.