Question

【题目】如图，△ABC为等边三角形，点D、E分别在AC、AB上，且AD＝BE，连接BD、CE交于点P，在△ABC外部作∠ABF＝∠ABD，过点A作AF⊥BF于点F，若∠ADB＝∠ABF+90°，BF﹣AF＝3，则BP＝_____．

Answer 1

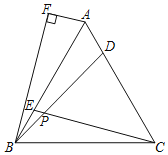
【答案】3﹣

【解析】

如图，在FB上取一点G，使得FG＝FA，作GF⊥AB于F，在FB上取一点H，使得GH＝HB，连接GH，在FB上取一点K，使得∠BAK＝45°，连接AK．证明△CBE≌△BAD（SAS），推出∠ABE＝∠BCE，推出∠DPC＝∠PCB+∠PBC＝∠PBC+∠ABD＝60°，由∠ADB＝∠ABF+90°＝∠DCB+∠DBC＝60°+60°﹣∠BCP＝120°﹣∠ABF，可得∠ABF＝15°，解直角三角形求出AK，再证明BP＝AK即可解决问题．

解：如图，在FB上取一点G，使得FG＝FA，作GT⊥AB于T，在FB上取一点H，使得GH＝HB，连接GH，在FB上取一点K，使得∠BAK＝45°，连接AK．

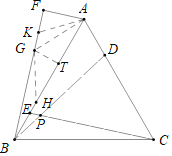
∵△ABC是等边三角形，

∴AB＝BC＝AC，

∠CBE＝∠BAD＝60°，

∵AD＝BE，

∴△CBE≌△BAD（SAS），

∴∠ABE＝∠BCE，

∴∠DPC＝∠PCB+∠PBC＝∠PBC+∠ABD＝60°

∵∠ADB＝∠ABF+90°＝∠DCB+∠DBC＝60°+60°﹣∠BCP＝120°﹣∠ABF，

∴∠ABF＝15°，

∵HG＝HB，

∴∠HGB＝∠HBG＝15°，

∴∠GHT＝∠HGB+∠HBG＝30°，设GT＝a，则GH＝BH＝2a，TH＝a，

∵BF﹣AF＝3，FA＝FG，

∴BG＝3，

在Rt△BGT中，∵BG2＝GT2+BT2，

∴a2+（2a+a）2＝9，

解得a＝，

∴TG＝，AG＝2TG＝，

∴AF＝FG＝，

∴AK＝，

∵∠BCP＝∠ABK，BC＝BA，∠CBP＝45°＝∠BAK，

∴△BCP≌△BAK（ASA），

∴BP＝CK＝3﹣．

故答案为：3﹣；