题目内容
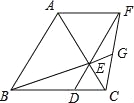
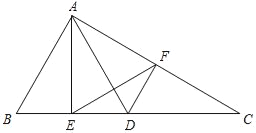
【题目】已知，如图1，将
绕点
旋转
得到
，延长线于点
，使得
，连接
．
（1）求证：四边形
是平行四边形；
（2）如图2，点
是边
上任意一点（点与点
、不重合），连接
交
于点
，连接
，过点
作
，交于点
．
①求证：
；
②当点是边中点时，恰有
（
为正整数），求的值．
【答案】（1）证明见解析
（2）①证明见解析 ②n=4
【解析】
（1）利用两线段平行且相等证明平行四边形．
（2）①由
，根据相似比即可求得数量关系．
②由，
，可导出相关线段的数量关系，即可求出结果．
解：（1）由题意可得
，点D、E、F共线
∴
，AD=BF
∴AD∥CF
又∵
∴
∴四边形
是平行四边形．
（2）①∵
∴
∴
由①得
∴
∴
∴
②∵
,
∴
∴
∵
是
边中点
∴BG=
BC
∴GF=
BC=AD
∴
，即HD=
HF
∵
∴
，即DK=HF
∴
∴
∴HD=4HK
∴n=4
练习册系列答案
相关题目
【题目】一家健身俱乐部收费标准为180元/次，若购买会员年卡，可享受如下优惠：
会员年卡类型 | 办卡费用（元） | 每次收费（元） |
A类 | 1500 | 100 |
B类 | 3000 | 60 |
C类 | 4000 | 40 |
例如，购买A类会员年卡，一年内健身20次，消费
元，若一年内在该健身俱乐部健身的次数介于50-60次之间，则最省钱的方式为（ ）
A.购买A类会员年卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
