题目内容
【题目】已知抛物线![]() 和
和![]()
(1)如何将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ?
?
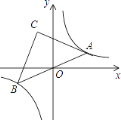
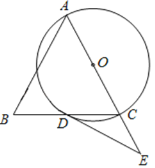
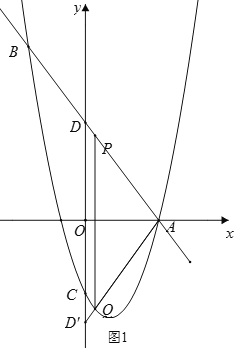
(2)如图1,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,交抛物线
,交抛物线![]() 于另一点
于另一点![]() .请你在线段
.请你在线段![]() 上取点
上取点![]() ,过点
,过点![]() 作直线
作直线![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连接
,连接![]()

①若![]() ,求点
,求点![]() 的横坐标
的横坐标
②若![]() ,直接写出点
,直接写出点![]() 的横坐标
的横坐标
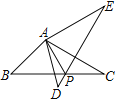
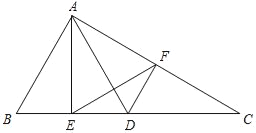
(3)如图2,![]() 的顶点
的顶点![]() 、
、![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在点
在点![]() 右边,两条直线
右边,两条直线![]() 、
、![]() 与抛物线
与抛物线![]() 均有唯一公共点,
均有唯一公共点,![]() 、
、![]() 均与
均与![]() 轴不平行.若
轴不平行.若![]() 的面积为2,设
的面积为2,设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求
,求![]() 与
与![]() 的数量关系
的数量关系

【答案】(1)见解析;(2)①点![]() 的横坐标为
的横坐标为![]() .②
.②![]() .(3)
.(3)![]() .
.
【解析】
(1)根据两个抛物线的顶点坐标即可确定平移方式;
(2)①如图1,设抛物线![]() 与
与![]() 轴交于
轴交于![]() 点,直线
点,直线![]() 与
与![]() 轴交于
轴交于![]() 点,确定出点A、C、D的坐标,进而由
点,确定出点A、C、D的坐标,进而由![]() ,
,![]() 轴,可得
轴,可得![]() ,
,![]() 两点关于
两点关于![]() 轴对称,设
轴对称,设![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,从而可得直线
,从而可得直线![]() 的解析式为
的解析式为![]() ,继而解方程组
,继而解方程组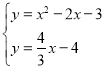 即可求得答案;
即可求得答案;
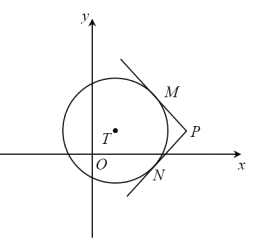
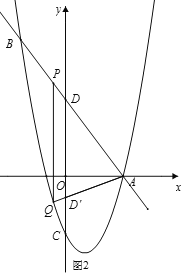
②如图2,![]() ,设P
,设P![]() ,Q
,Q![]() ,分别表示出PQ长,AP2,再根据AP=PQ,得到关于m的方程,解方程即可求得答案;
,分别表示出PQ长,AP2,再根据AP=PQ,得到关于m的方程,解方程即可求得答案;
(3)如图3,分别求出直线NE、NE、MN的解析式,作![]() 轴交
轴交![]() 于
于![]() 点,表示出EF的长,继而根据三角形面积公式进行求解即可.
点,表示出EF的长,继而根据三角形面积公式进行求解即可.
(1)抛物线![]() 的顶点坐标是(1,-4),
的顶点坐标是(1,-4),
抛物线![]() 的顶点坐标是(0,0),
的顶点坐标是(0,0),
所以将![]() 先向左平移1个单位长度,再向上平移4个单位长度得到
先向左平移1个单位长度,再向上平移4个单位长度得到![]() 或将
或将![]() 先向上平移4个单位长度,再向左平移1个单位长度得到
先向上平移4个单位长度,再向左平移1个单位长度得到![]() ;
;
(2)①如图1,设抛物线![]() 与
与![]() 轴交于
轴交于![]() 点,直线
点,直线![]() 与
与![]() 轴交于
轴交于![]() 点,
点,
![]() ,
,
当x=0时,y=-3,
当y=0时,x=-1或x=3,
∴![]() ,
,![]() ,
,
∵直线![]() 经过
经过![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,
,![]() 轴,∴
轴,∴![]() ,
,![]() 两点关于
两点关于![]() 轴对称,
轴对称,
设![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,则
,则![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由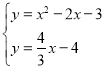 ,得,
,得,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的横坐标为
的横坐标为![]() ;
;
②如图2,![]() ,
,
设P![]() ,Q
,Q![]() ,
,
则有PQ=![]() -
-![]() =-m2+
=-m2+![]() m+7,
m+7,
又∵A(3,0),
∴AP2=(3-m)2+(![]() )2=
)2=![]() ,
,
∵AP=PQ,
∴(-m2+![]() m+7)2=
m+7)2=![]() ,
,
∴[![]() (m-3)(3m+7)]2=
(m-3)(3m+7)]2=![]() ,
,
∴(m-3)2(3m+7)2=25(m-3)2,
∵m≠3,
∴(3m+7)2=25,
∴m1=-![]() ,m2=-4(舍去),
,m2=-4(舍去),
∴m=-![]() ;
;
(3)如图3,
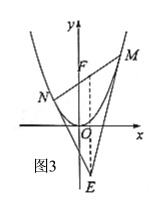
∵![]() ,∴
,∴![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∵![]() ,∴
,∴![]() ,
,
由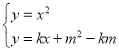 得,
得,![]() ,
,
依题意有,![]() ,∴
,∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
同理,直线![]() 的解析式为
的解析式为![]() ,
,
由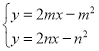 得,
得,![]() ,
,
∵![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
作![]() 轴交
轴交![]() 于
于![]() 点,则
点,则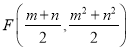 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
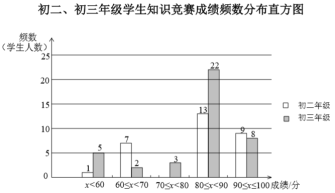
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.