题目内容
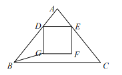
【题目】如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 上的两个动点(
上的两个动点(![]() 不与
不与![]() 重合),且保持
重合),且保持![]() ,以
,以![]() 为边,在点 A 的异侧作正方形
为边,在点 A 的异侧作正方形![]() .
.
(1)试求![]() 的面积;
的面积;
(2)当边![]() 与
与![]() 重合时,求正方形
重合时,求正方形![]() 的边长;
的边长;
(3)设![]() 与正方形
与正方形![]() 重叠部分的面积为
重叠部分的面积为![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的范围;
的范围;
(4)当![]() 是等腰三角形时,请直接写出
是等腰三角形时,请直接写出![]() 的长.
的长.
【答案】(1)12;(2)![]() ;(3)当0 <x≤2时,
;(3)当0 <x≤2时,![]() ,当2 < x<5时,
,当2 < x<5时,![]() ;(4)
;(4)![]() .
.
【解析】
(1)作底边上的高,利用勾股定理求出高就可以求出面积.
(2)根据DE∥BC,得到△ADE∽△ABC,再根据相似三角形对应高的比等于相似比即可求出边DE的长度.
(3)可以分为正方形在三角形内部和不全在内部两种情况求解,全在内部时,利用三角形相似得![]() ,求出DE,再求重叠部分正方形的面积,不全在内部时先求出长DE,再利用DG∥AH,求出宽.
,求出DE,再求重叠部分正方形的面积,不全在内部时先求出长DE,再利用DG∥AH,求出宽.
(4)当△BDG是等腰三角形时,分BD=DG,BD=BG,DG=BG三种情况写出AD的长.
解:(1)过A作![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
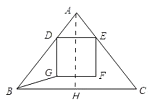
(2)令此时正方形的边长为a,如图
∵DE∥BC,
∴![]()
即![]()
![]() ,
,
(3)当DE=![]() 时,由△ADE∽△ABC得
时,由△ADE∽△ABC得![]() ,解得AD=2,
,解得AD=2,
当0 < x ≤ 2时,正方形全部在三角形内部,由![]() 得:
得:![]() ,DE=
,DE=![]() ,
,
∴![]() (0 < x ≤ 2);
(0 < x ≤ 2);
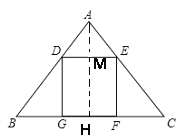
当 2 < x < 5 时,如图,DE=![]() ,BD=5-x
,BD=5-x
∵sin∠B=![]()
即![]()
∴DM=![]() ,
,

∴![]() (2 < x < 5);
(2 < x < 5);
(4)当△BDG是等腰三角形时,设AD=x,当BD=DG,
此时正方形不全部在三角形内部,
∵BD=5x,
由(3)可知DG=DE=![]() ,
,
∴5x=![]()
解得x=![]() ,
,
∴AD=![]() ;
;
当DB=BG时,BD=5-x,DG=![]()
∵cos∠B=![]()
即![]()
∴BM=![]() =3-
=3-![]() x
x
又DM=![]() ,
,
∴MG=DG-DM=![]() -[
-[![]() ]=2x-4
]=2x-4
∴BG2=BM2+MG2=(3-![]() x)2+(2x-4)2
x)2+(2x-4)2
∵DB=BG
∴BD2=BG2,
即(5-x)2=(3-![]() x)2+(2x-4)2
x)2+(2x-4)2
解得x=![]() (x=0舍去)
(x=0舍去)
∴AD=![]() ;
;

当DG=BG,同理DG2=BG2,
即(![]() )2=(3-
)2=(3-![]() x)2+(2x-4)2
x)2+(2x-4)2
解得x=![]() (x=5舍去)
(x=5舍去)
∴AD=![]() ;
;
故AD=![]() ,
,![]() ,
,![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
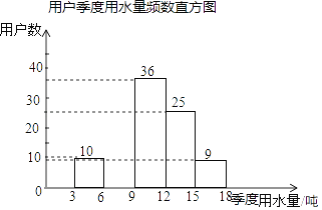
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=_______,n=________;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?