题目内容
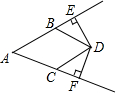如图，已知AB=AC，BD=CD，DE⊥AB，交AB的延长线于点E，DF⊥AC，交AC的延长线于点F．求证：DE=DF．分析：如图，连接AD、先证△ABD≌△ACD（SSS），则对应角∠BAD=∠CAD．然后利用角平分线的性质证得结论．
解答：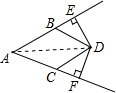
证明：如图，连接AD．
在△ABD与△ACD中，
，
∴△ABD≌△ACD（SSS），
∴∠BAD=∠CAD，即AD是∠BAC的平分线，
又∵DE⊥AB，DF⊥AC，
∴DE=DF．
证明：如图，连接AD．在△ABD与△ACD中，
|
∴△ABD≌△ACD（SSS），
∴∠BAD=∠CAD，即AD是∠BAC的平分线，
又∵DE⊥AB，DF⊥AC，
∴DE=DF．
点评：本题考查了全等三角形的判定与性质，角平分线的性质．角的平分线上的点到角的两边的距离相等．
练习册系列答案
相关题目
如图，已知AB⊥AC，AD⊥AE，AB=AC，AD=AE，则∠BFD的度数是（ ）| A、60° | B、90° | C、45° | D、120° |
10、如图，已知AB=AC，D是BC的中点，E是AD上的一点，图中全等三角形有几对（ ）
26、如图，已知AB=AC，AD=AE．求证BD=CE．
2、如图，已知AB=AC，AD=AE，BD=EC，则图中有
如图，已知AB=AC，BC=CD=AD，求∠B的值．