题目内容
 (2012•朝阳)如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(2012•朝阳)如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.
分析:(1)有正方形的性质和已知条件证明∠BAE=∠FEC即可证明:△ABE∽△ECF;
(2)连接AF,延长AE于DC的延长线相交于点H,当点E在BC中点位置时,通过证明三角形全等和等腰三角形的性质以及平行线的性质即可证明∠BAE=∠EAF.
(2)连接AF,延长AE于DC的延长线相交于点H,当点E在BC中点位置时,通过证明三角形全等和等腰三角形的性质以及平行线的性质即可证明∠BAE=∠EAF.
解答: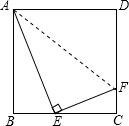 (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)E是中点时,∠BAE=∠EAF,
理由如下: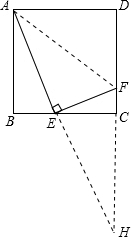
连接AF,延长AE于DC的延长线相交于点H,
∵E为BC中点,
∴BE=CE,
∵AB∥DH,
∴∠B=∠ECH,
∵∠AEB=∠CEH,
∴△ABE≌△HCE,
∴AE=EH,
∵EF⊥AH,
∴△AFH是等腰三角形,
∴∠EAF=∠H,
∵AB∥DH,
∴∠H=∠BAE,
∴∠BAE=∠EAF,
∴当点E在BC中点位置时,∠BAE=∠EAF.
 (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)E是中点时,∠BAE=∠EAF,
理由如下:

连接AF,延长AE于DC的延长线相交于点H,
∵E为BC中点,
∴BE=CE,
∵AB∥DH,
∴∠B=∠ECH,
∵∠AEB=∠CEH,
∴△ABE≌△HCE,
∴AE=EH,
∵EF⊥AH,
∴△AFH是等腰三角形,
∴∠EAF=∠H,
∵AB∥DH,
∴∠H=∠BAE,
∴∠BAE=∠EAF,
∴当点E在BC中点位置时,∠BAE=∠EAF.
点评:本题考查了正方形的性质、相似三角形的判断和性质以及等腰三角形的判断和性质的综合运用,解答本题的关键是熟练掌握正方形的性质和相似三角形的各种判断方法,此题难度不大.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 (2012•朝阳)如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费
(2012•朝阳)如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费 (2012•朝阳)如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧
(2012•朝阳)如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧
 (2012•朝阳)如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,则线段AC扫过的扇形所围成的圆锥体的底面半径是
(2012•朝阳)如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,则线段AC扫过的扇形所围成的圆锥体的底面半径是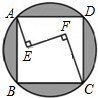 (2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为
(2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为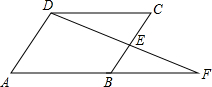 (2012•朝阳)如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF,请你添加一个条件(不需再添加任何线段或字母),使之能推出四边形ABCD为平行四边形,请证明.你添加的条件是
(2012•朝阳)如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF,请你添加一个条件(不需再添加任何线段或字母),使之能推出四边形ABCD为平行四边形,请证明.你添加的条件是