题目内容
（2012•朝阳）如图，△ABC三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将△ABC绕点C顺时针旋转到△A′B′C的位置，且A′、B′仍落在格点上，则线段AC扫过的扇形所围成的圆锥体的底面半径是
| ||
| 4 |
| ||
| 4 |
分析：首先求得扇形的半径和圆心角，然后求得扇形的弧长，然后根据弧长等于底面的半径求得半径即可．
解答：解：根据题意得：CA=
=
=
，
∠ACA′=90°，
故扇形的弧长为：
=
，
设圆锥的半径为r，则2πr=
，
解得：r=
，
故答案为：
．
| AB2+BC2 |
| 22+32 |
| 13 |
∠ACA′=90°，
故扇形的弧长为：
90π×
| ||
| 180 |
| ||
| 2 |
设圆锥的半径为r，则2πr=
| ||
| 2 |
解得：r=
| ||
| 4 |
故答案为：
| ||
| 4 |
点评：本题考查了圆锥的计算，弧长的公式及旋转的性质，解题的关键是牢记弧长的公式及扇形与圆锥的有关元素的对应．
练习册系列答案
相关题目
（2012•朝阳）如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y（元）与通话时间t（分钟）之间的函数关系，则通话8分钟应付电话费
（2012•朝阳）如图已知P为⊙O外一点，PA为⊙O的切线，B为⊙O上一点，且PA=PB，C为优弧
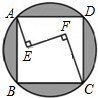（2012•朝阳）如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE=4，EF=8，FC=12，则正方形与其外接圆形成的阴影部分的面积为
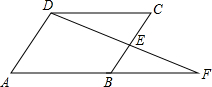（2012•朝阳）如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，AB=BF，请你添加一个条件（不需再添加任何线段或字母），使之能推出四边形ABCD为平行四边形，请证明．你添加的条件是