题目内容
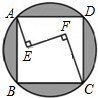（2012•朝阳）如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE=4，EF=8，FC=12，则正方形与其外接圆形成的阴影部分的面积为80π-160
80π-160
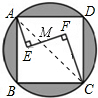
．分析：首先连接AC，则可证得△AEM∽△CFM，根据相似三角形的对应边成比例，即可求得EM与FM的长，然后由勾股定理求得AM与CM的长，则可求得正方形与圆的面积，则问题得解．
解答：解：连接AC，
∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF（对顶角相等），
∴△AEM∽△CFM，
∴
=
，
∵AE=4，FC=12，
∴
=
，
∴EM=2，FM=6，
在Rt△AEM中，AM=
=2
，
在Rt△FCM中，CM=
=6
，
∴AC=8
，
在Rt△ABC中，AB=AC•sin45°=8
×
=4
，
∴S正方形ABCD=AB2=160，
圆的面积为：π•（
）2=80π，
∴正方形与其外接圆之间形成的阴影部分的面积为80π-160．
故答案为：80π-160．
∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF（对顶角相等），
∴△AEM∽△CFM，
∴
| AE |
| CF |
| EM |
| FM |
∵AE=4，FC=12，
∴
| EM |
| FM |
| 1 |
| 3 |
∴EM=2，FM=6，
在Rt△AEM中，AM=
| AE2 +EM2 |
| 5 |
在Rt△FCM中，CM=
| CF2 +FM2 |
| 5 |
∴AC=8
| 5 |
在Rt△ABC中，AB=AC•sin45°=8
| 5 |
| ||
| 2 |
| 10 |
∴S正方形ABCD=AB2=160，
圆的面积为：π•（
8
| ||
| 2 |
∴正方形与其外接圆之间形成的阴影部分的面积为80π-160．
故答案为：80π-160．
点评：此题考查了相似三角形的判定与性质，正方形与圆的面积的求解方法，以及勾股定理的应用．此题综合性较强，解题时要注意数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2012•朝阳）如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y（元）与通话时间t（分钟）之间的函数关系，则通话8分钟应付电话费
（2012•朝阳）如图已知P为⊙O外一点，PA为⊙O的切线，B为⊙O上一点，且PA=PB，C为优弧
（2012•朝阳）如图，△ABC三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将△ABC绕点C顺时针旋转到△A′B′C的位置，且A′、B′仍落在格点上，则线段AC扫过的扇形所围成的圆锥体的底面半径是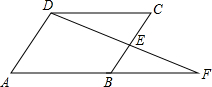
（2012•朝阳）如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，AB=BF，请你添加一个条件（不需再添加任何线段或字母），使之能推出四边形ABCD为平行四边形，请证明．你添加的条件是