题目内容
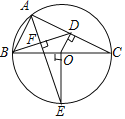
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=_____.
【答案】4![]() .
.
【解析】
根据垂径定理得到AD=DC,由等腰三角形的性质得到AB=2OD=2×2=4,得到∠BAE=∠CAE=![]() ∠BAC=
∠BAC=![]() ×90°=45°,求得∠ABD=∠ADB=45°,求得AD=AB=4,于是得到DC=AD=4,根据勾股定理即可得到结论.
×90°=45°,求得∠ABD=∠ADB=45°,求得AD=AB=4,于是得到DC=AD=4,根据勾股定理即可得到结论.
∵OD⊥AC,
∴AD=DC,
∵BO=CO,
∴AB=2OD=2×2=4,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵OE⊥BC,
∴∠BOE=∠COE=90°,
∴![]() ,
,
∴∠BAE=∠CAE=![]() ∠BAC=
∠BAC=![]() ×90°=45°,
×90°=45°,
∵EA⊥BD,
∴∠ABD=∠ADB=45°,
∴AD=AB=4,
∴DC=AD=4,
∴AC=8,
∴BC=![]() =
=![]() =4
=4![]() .
.
故答案为:4![]() .
.

练习册系列答案
相关题目