题目内容
【题目】在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.

(1)求抛物线的解析式.
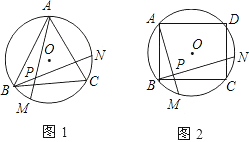
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,G是线段OC上一个动点,连接DG,过点G作GM⊥DG交AC于点M,过点M作射线MN,使∠NMG=60°,交射线GD于点N;过点G作GH⊥MN,垂足为点H,连接BH.请直接写出线段BH的最小值.
【答案】(1)y=﹣x2+3x+4;(2)点P的坐标为(1+![]() ,4+
,4+![]() )或(1﹣
)或(1﹣![]() ,4﹣
,4﹣![]() );(3)BH最小=
);(3)BH最小=![]() .
.
【解析】
(1)利用待定系数法求解可得;
(2)作PE∥x轴,交AB于点E,由![]() 且△AQD与△APQ是等高的两个三角形知
且△AQD与△APQ是等高的两个三角形知![]() ,证△PQE∽△DQB得
,证△PQE∽△DQB得![]() ,据此求得PE=2,求得直线AB的解析式为y=x+1,设E(x,x+1),知P(x-2,x+1),将点P坐标代入
,据此求得PE=2,求得直线AB的解析式为y=x+1,设E(x,x+1),知P(x-2,x+1),将点P坐标代入![]() 求得x的值,从而得出答案;
求得x的值,从而得出答案;
(3)证∠GHM=90°,再证点C、G、H、M共圆得∠GCH=∠GMH=60°,据此知点H在与y轴夹角为60°的定直线上,从而得BH⊥CH时,BH最小,作HP⊥x轴,并延长PH交AC于点Q,证∠BHP=∠HCM=30°,设OP=a,知CQ=a,从而得QH=![]() ,BP=1+a,在Rt△BPH中,得出HP=
,BP=1+a,在Rt△BPH中,得出HP=![]() (a+1),BH=2(1+a),根据QH+HP=AD=4可求得a的值,从而得出答案.
(a+1),BH=2(1+a),根据QH+HP=AD=4可求得a的值,从而得出答案.
(1)将点A(3,4),B(﹣1,0)代入y=ax2+bx+4,
得:![]() ,
,
解得![]() ,
,
∴y=﹣x2+3x+4;
(2)如图1,过点P作PE∥x轴,交AB于点E,
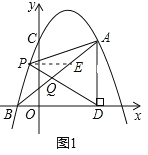
∵A(3,4),AD⊥x轴,
∴D(3,0),
∵B(﹣1,0),
∴BD=3﹣(﹣1)=4,
∵S△AQD=2S△APQ,△AQD与△APQ是等高的两个三角形,
∴![]() ,
,
∵PE∥x轴,
∴△PQE∽△DQB,
∴![]() ,
,
∴![]() ,
,
∴PE=2,
∴可求得直线AB的解析式为y=x+1,
设E(x,x+1),则P(x﹣2,x+1),
将点P坐标代入y=﹣x2+3x+4,得:﹣(x-2)2+3(x-2)+4=x+1,
解得x1=3+![]() ,x2=3﹣
,x2=3﹣![]() ,
,
当x=3+![]() 时,x﹣2=3+
时,x﹣2=3+![]() ﹣2=1+
﹣2=1+![]() ,x+1=3+
,x+1=3+![]() +1=4+
+1=4+![]() ,
,
∴点P(1+![]() ,4+
,4+![]() );
);
当x=3﹣![]() 时,x﹣2=3﹣
时,x﹣2=3﹣![]() ﹣2=1﹣
﹣2=1﹣![]() ,x+1=3﹣
,x+1=3﹣![]() +1=4﹣
+1=4﹣![]() ,
,
∴P(1﹣![]() ,4﹣
,4﹣![]() ),
),
∵点P是直线AB上方抛物线上的一个动点,
∴﹣1<x﹣2<3,
∴点P的坐标为(1+![]() ,4+
,4+![]() )或(1﹣
)或(1﹣![]() ,4﹣
,4﹣![]() );
);
(3)由(1)得,抛物线的解析式为y=﹣x2+3x+4,
∴C(0,4),
∵A(3,4),
∴AC∥x轴,
∴∠OCA=90°,
∴GH⊥MN,
∴∠GHM=90°,
在四边形CGHM中,∠GCM+∠GHM=180°,
∴点C、G、H、M共圆,
如图2,连接CH,
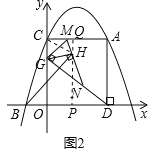
则∠GCH=∠GMH=60°,
∴点H在与y轴夹角为60°的定直线上,
∴当BH⊥CH时,BH最小,过点H作HP⊥x轴于点P,并延长PH交AC于点Q,
∵∠GCH=60°,
∴∠HCM=30°,
又BH⊥CH,
∴∠BHC=90°,
∴∠BHP=∠HCM=30°,
设OP=a,则CQ=a,
∴QH=![]() a,
a,
∵B(﹣1,0),
∴OB=1,
∴BP=1+a,
在Rt△BPH中,HP=![]() =
=![]() (a+1),BH=
(a+1),BH=![]() =2(1+a),
=2(1+a),
∵QH+HP=AD=4,
∴![]() a+
a+![]() (a+1)=4,
(a+1)=4,
解得a=![]() ,
,
∴BH最小=2(1+a)=![]() .
.