Question

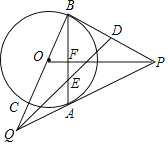
【题目】如图，∠A+∠B+∠C+∠D+∠E+∠F=_______度.

Answer 1

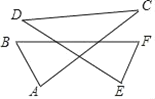
【答案】360°

【解析】

先根据图形的特点，将∠A +∠B、∠C +∠D和∠E +∠F分别转化成和它不相邻的外角，再根据邻补角的定义转化为一个三角形的内角，然后利用三角形的内角和定理求解即可.

如图，记BF交DE于G，交AC于H，DE交AC于I ，

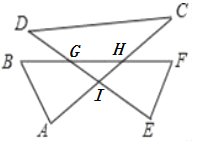
∵∠FHI＝∠A +∠B，

∴∠GHI＝180°-∠FHI＝180°-（∠A+ ∠B），

∵∠AIG＝∠C +∠D，

∴∠GIH＝180°-∠AIG＝180°-（∠C +∠D），

∵∠BGI＝∠E +∠F，

∴∠HGI＝180°-∠BGI＝180°-（∠E +∠F），

∵∠GHI+∠GIH +∠HGI＝180°，

∴180°-（∠A +∠B）+ 180°-（∠C +∠D）+ 180°-（∠E+ ∠F）＝180°，

∴∠A+∠B+∠C+∠D+∠E+∠F＝360°.