题目内容
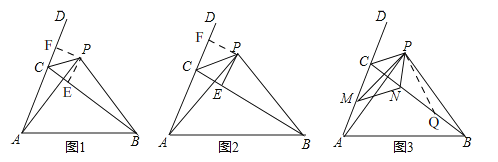
【题目】如图点P为△ABC的外角∠BCD的平分线上一点,PA=PB.
(1)如图1,求证:∠PAC=∠PBC;
(2)如图2,作PE⊥BC于E,若AC=5,BC=11,则![]() = ;
= ;
(3)如图3,若M、N分别是边AC、BC上的点,且∠MPN=![]() ∠APB,则线段AM、MN、BN 之间有何数量关系,并说明理由.
∠APB,则线段AM、MN、BN 之间有何数量关系,并说明理由.

【答案】(1)答案见解析;(2)3:8;(3)AM+MN=BN.
【解析】试题分析:(1)先利用角平分线定理判断出PE=PF,进而判断出Rt△PAF≌Rt△PEB,即可得出结论;
(2)先判断出△PCF≌△PCE,进而得出CF=CE,而Rt△PAF≌Rt△PEB得出AF=BE即可得出AC+CF=BC﹣CE,进而求出CE=CF=3,即可求出结论;
(3)先判断出△PMA≌△PQB,进而得出∠APB=∠MPQ,即可判断出△MPN≌△QPC,得出MN=QN即可得出结论.
试题解析:解:(1)如图1,过点P作PE⊥BC于E,PF⊥AC于F,∵PC平分∠DCB,∴PE=PF,在Rt△PAF和Rt△PEB中,∵PF=PE,PA=PB,∴Rt△PAF≌Rt△PEB,∴∠PAC=∠PBC;
(2)如图2,过点P作PF⊥AC于F,∵PE⊥BC,CP是∠BCD的平分线,∴PE=PF,∠PCF=∠PCE,∵PC=PC,∴△PCF≌△PCE,∴CF=CE,由(1)知,Rt△PAF≌Rt△PEB,∴AF=BE,∵AF=AC+CF,BE=BC﹣CE,∴AC+CF=BC﹣CE,∴5+CF=11﹣CE,∴CE=CF=3,∵△PFC≌△PEC,∴S△PFC=S△PEC,∵Rt△PAF≌Rt△PEB,∴S△PAF=S△PEB,∴S△PCE:S△PBE=S△PFC:S△PFA=![]() CF×PF:
CF×PF: ![]() AC×PF=CF:AC=3:(3+5)=3:8;
AC×PF=CF:AC=3:(3+5)=3:8;
(3)如图3,在BC上截取BQ=AM,在△PMA和△PQB中,∵PA=PB,∠PAM=∠PBQ,MA=BQ,∴△PMA≌△PQB,∴PM=PQ,∠MPA=QPB,∴∠APM+∠QPB=∠APN+∠MPA,即:∠APB=∠MPQ,∵∠MPN=![]() ∠APB,∴∠MPN=
∠APB,∴∠MPN=![]() ∠MPQ,∴∠MPN=∠QPN,在△MPN和△QPC中,∵PN=PN,∠MPN=∠QPN,MP=QP,∴△MPN≌△QPC,∴MN=QN,∴BM=AM+MN.
∠MPQ,∴∠MPN=∠QPN,在△MPN和△QPC中,∵PN=PN,∠MPN=∠QPN,MP=QP,∴△MPN≌△QPC,∴MN=QN,∴BM=AM+MN.

【题目】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
选手 | 甲 | 乙 | 丙 | 丁 |
方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁
