题目内容
如图，在平面直角坐标系中直线y=x﹣2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．
（1）求反比例函数的关系式；
（2）将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C，且△ABC的面积为18，求平移后的直线的函数关系式．
解：（1）将B坐标代入直线y=x﹣2中得：m﹣2=2，解得：m=4，
∴B（4，2），即BE=4，OE=2。
设反比例解析式为
，
将B（4，2）代入反比例解析式得：k=8，
∴反比例解析式为
。
（2）设平移后直线解析式为y=x+b，C（a，a+b），
对于直线y=x﹣2，令x=0求出y=﹣2，得到OA=2，
过C作CD⊥y轴，过B作BE⊥y轴，
将C坐标代入反比例解析式得：a（a+b）=8①，
∵
，
∴
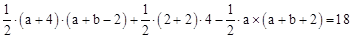②。
①②联立，解得：b=7。
∴平移后直线解析式为y=x+7。
解析
练习册系列答案
相关题目
的图像与一次函数
的图像交于点A(ｍ，2)，点B(－2, n )，一次函数图像与y轴的交点为C.求△AOC的面积。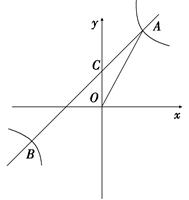
的图象在第二象限交与点C，如果点A为的坐标为（2，0），B是AC的中点．
的图象有一个公共点A（1，2）．
经过第一、二、三象限，与y轴交于点B，点A（2，t）在这条直线上，连接AO，△AOB的面积等于1．
（
是常量，
）的图像经过点A，求这个反比例函数的解析式．
的图象与一次函数
的图象交于A
、B
两点，连结AO。
的图象交于点A，与x轴交于点B，AC⊥x轴于点C，
，AB=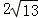
，OB=OC．