题目内容
【题目】一仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施，该设施的下部ABCD是矩形，其中AB=2米，BC=
米，上部△CDG是等边三角形，固定点E为AB的中点。△EMN是由电脑控制其变化的三角通风窗（阴影部分均不通风），MN（MN可与CD重合）是可以沿设施边框上下滑动且始终保持与AB平行的伸缩横杆。（当MN在DC上方时，MD的长度是MN到DC距离的
倍）
（1）当MN和AB之间的距离为0.5米时，求此时 △EMN的面积；
（2）设MN与AB之间的距离为x米，求△EMN的面积S（平方米）与x的函数关系式；
（3）探究△EMN的面积S（平方米）有无最大值，若有，求出这个最大值；若无，请说明理由。
【答案】（1）0.5平方米；（2）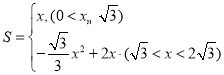
；（3）S有最大值，最大值为
平方米
【解析】
（1）根据题意得出当MN和AB之间的距离为0.5米时，MN应位于DC下方，且此时△EMN中MN边上的高为0.5米,可得出三角形EMN的面积．
（2）分两种情况解答（0＜x≤
；＜x＜2）．①当0＜x≤时，可直接得出三角形的面积函数；②当＜x＜
时，连接EG，交CD于点F，交MN于点H，先求FG，再证△MNG∽△DCG，继而得出△EMN面积与x的函数；
（3）分两种情况解答：①当0＜x≤时， S=x，由一次函数性质可得S的最大值；②当＜x＜2时，由二次函数性质可知，在对称轴时取得最大值，比较大小即可得出结论．
解：（1）由题意，当MN和AB之间的距离为0.5米时，MN应位于DC下方如图1
此时△EMN中MN边上的高为0.5米．
在ABCD是矩形中，AB=CD=MN=2米，BC=AD=米，
∴S△EMN=
×2×0.5=0.5（平方米）．
即△EMN的面积为0.5平方米．
（2）①如图1所示，当MN在矩形区域滑动，即0＜x≤时，
△EMN的面积S=×2×x=x；
②如图2所示，当MN在三角形区域滑动，即＜x＜时，
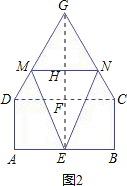
连接EG，交CD于点F，交MN于点H，
∵E为AB中点，
∴F为CD中点，GF⊥CD，且FG=．
∴EG=
，
∴MN＝4-
∴△EMN的面积S=
∴
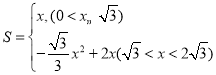
（3）①当0＜x≤时， S=x，
∴0＜S≤；
∴S的最大值=
②当＜x＜时，
S=
当
时，S有最大值，且最大值为：
∴综上所述：S有最大值，最大值为平方米．
